题目内容
在平面直角坐标系中,定义以原点为圆心,以
为半径的圆O为椭圆C:
+
=1(a>b>0)的“准圆”.已知椭圆C:
+
=1的离心率为
,直线l:2x-y+5=0与椭圆C的“准圆”相切.
(1)求椭圆C的方程;
(2)P为椭圆C的右准线上一点,过点P作椭圆C的“准圆”的切线段PQ,点F为椭圆C的右焦点,求证:|PQ|=|PF|
(3)过点M(-
,0)的直线与椭圆C交于A,B两点,为Q椭圆C的左顶点,是否存在直线l使得△QAB为直角三角形?
| a2+b2 |
| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 3 |
(1)求椭圆C的方程;
(2)P为椭圆C的右准线上一点,过点P作椭圆C的“准圆”的切线段PQ,点F为椭圆C的右焦点,求证:|PQ|=|PF|
(3)过点M(-
| 6 |
| 5 |
分析:(1)由于直线l:2x-y+5=0与椭圆C的“准圆”相切,利用点到直线的距离公式可得
=
=
,即a2+b2=5,联立
,解得即可;
(2)椭圆C的准线方程为x=
=3,可设P(3,t).利用两点间的距离公式可得|PF|2.由于PQ与椭圆C的准圆x2+y2=5相切于点Q,利用勾股定理可得|PQ|2=|OP|2-r2,即可证明结论.
(3)假设存在直线l使得△QAB为直角三角形,只有可能∠AQB=90°.设A(x1,y1),B(x2,y2).设直线l的方程为:my=x+
,与椭圆的方程联立得到根与系数的关系,令
•
=0,若解出m的值证明存在△QAB为直角三角形,否则不存在.
| a2+b2 |
| 5 | ||
|
| 5 |
|
(2)椭圆C的准线方程为x=
| a2 |
| c |
(3)假设存在直线l使得△QAB为直角三角形,只有可能∠AQB=90°.设A(x1,y1),B(x2,y2).设直线l的方程为:my=x+
| 6 |
| 5 |
| AQ |
| BQ |
解答:解:(1)∵直线l:2x-y+5=0与椭圆C的“准圆”相切,∴
=
=
,化为a2+b2=5,联立
,解得a2=3,b2=2,c=1.
∴椭圆C的方程为
+
=1;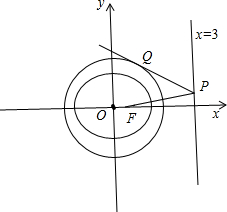
(2)如图所示,∵椭圆C的准线方程为x=
=3,可设P(3,t).∵椭圆C的焦点F(1,0),∴|PF|2=(3-1)2+(t-0)2=4+t2.
∵PQ与椭圆C的准圆x2+y2=5相切于点Q,∴|PQ|2=|OP|2-r2=32+t2-5=4+t2,
∴|PQ|2=|PF|2,∴|PQ|=|PF|.
(3)假设存在直线l使得△QAB为直角三角形,可能∠AQB=90°,∠QAB=90°,或∠QBA=90°
设A(x1,y1),B(x2,y2).
设直线l的方程为:my=x+
,联立
化为(75+50m2)y2-120my-78=0.
∴y1+y2=
,y1y2=
.
①由
•
=(x1+
,y1)•(x2+
,y2)=(my1-
+
,y1)•(my2-
+
,y2)
=(m2+1)y1y2+(
-
)m(y1+y2)+(
-
)2
=
+
+(
-
)2=0,
化为[(
-
)2×50-222]m2=78-75(
-
)2,无解,此时不存在直线l满足条件.
②令
•
=(x1+
,y1)•(x1+
,y1)=
+(
+
)x1+
+
=
+(
+
)x1+
+(2-
)=
+(
+
)x1+
=0,
∵△=(
+
)2-4×
×
>0,∴此时存在两个A点满足条件;
同理存在两个B点满足条件.
综上可知:存在四条直线l满足条件.
| a2+b2 |
| 5 | ||
|
| 5 |
|
∴椭圆C的方程为
| x2 |
| 3 |
| y2 |
| 2 |

(2)如图所示,∵椭圆C的准线方程为x=
| a2 |
| c |
∵PQ与椭圆C的准圆x2+y2=5相切于点Q,∴|PQ|2=|OP|2-r2=32+t2-5=4+t2,
∴|PQ|2=|PF|2,∴|PQ|=|PF|.
(3)假设存在直线l使得△QAB为直角三角形,可能∠AQB=90°,∠QAB=90°,或∠QBA=90°
设A(x1,y1),B(x2,y2).
设直线l的方程为:my=x+
| 6 |
| 5 |
|
∴y1+y2=
| 120m |
| 75+50m2 |
| -78 |
| 75+50m2 |
①由
| QA |
| QB |
| 3 |
| 3 |
| 6 |
| 5 |
| 3 |
| 6 |
| 5 |
| 3 |
=(m2+1)y1y2+(
| 3 |
| 6 |
| 5 |
| 3 |
| 6 |
| 5 |
=
| -78(1+m2) |
| 75+50m2 |
120•(
| ||||
| 75+50m2 |
| 3 |
| 6 |
| 5 |
化为[(
| 3 |
| 6 |
| 5 |
| 3 |
| 6 |
| 5 |
②令
| QA |
| MA |
| 3 |
| 6 |
| 5 |
| x | 2 1 |
| 3 |
| 6 |
| 5 |
6
| ||
| 5 |
| y | 2 1 |
| x | 2 1 |
| 3 |
| 6 |
| 5 |
6
| ||
| 5 |
2
| ||
| 3 |
| 1 |
| 3 |
| x | 2 1 |
| 3 |
| 6 |
| 5 |
10+6
| ||
| 5 |
∵△=(
| 3 |
| 6 |
| 5 |
| 1 |
| 3 |
10+6
| ||
| 5 |
同理存在两个B点满足条件.
综上可知:存在四条直线l满足条件.
点评:本题综合考查了椭圆的标准方程及其性质、直线与椭圆相交问题转化为方程联立得到根与系数的关系、直线与圆相切问题、勾股定理、向量垂直与数量积的关系等基础知识与基本技能方法,属于难题.

练习册系列答案
相关题目