题目内容
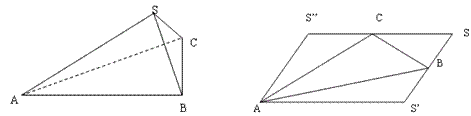
已知三棱锥S—ABC中,侧棱SA、SB、SC两两垂直,若将此三棱锥沿侧棱展成平面图形恰好可以形成一个边长为![]() 的正方形.
的正方形.
(1)求证:顶点![]() 在底面ABC的射影
在底面ABC的射影![]() 是底面
是底面![]() 的垂心;
的垂心; ![]()
![]()
(2)求二面角S-AB-C的大小.

(1)证明略(2)二面角S-AB-C的大小为![]()
解析:
(1)作![]() ,连AO、BO,
,连AO、BO,
因为侧棱SA、SB、SC两两垂直,易证![]() 、
、![]() 、
、
![]() .
.
所以![]() ,由三垂线定理的逆定理,AO
,由三垂线定理的逆定理,AO![]() BC,同理可证BO
BC,同理可证BO![]() AC.
AC.
所以O为高线的交点,即为![]() 垂心. …………………6分
垂心. …………………6分
(2)由于三棱锥的展开图成边长为![]() 正方形,则B、C分别
正方形,则B、C分别![]() 和
和![]() 的中点,
的中点,
即SB=SC=![]() ,所以SA=
,所以SA=![]() ,AB=AC=
,AB=AC=![]() ,BC=
,BC=![]() .
.
在三棱锥S—ABC中,过S作SD垂直AB于D,连CD。因为![]() ,
,
根据三垂线定理,CD![]() AB,所以
AB,所以![]() 即为二面角求二面角S-AB-C的平面角.
即为二面角求二面角S-AB-C的平面角.
在三角形SAB中,![]() ,SC=
,SC=![]() ,SA=
,SA=![]() ,AC=
,AC=![]() ,所以SD=
,所以SD=![]()
所以
![]() ,
,
即二面角S-AB-C的大小为![]() . …………………12分
. …………………12分

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目