题目内容
若i是虚数单位,设
=a+(b+1)i(a,b∈R),则复数z=a+bi在复平面内对应的点位于
| 1+i | 2-i |
第四象限
第四象限
.分析:化简
为
+
i,再根据两个复数相等的充要条件求得a、b的值,即可得到复数z=a+bi在复平面内对应的点的坐标,从而得出结论.
| 1+i |
| 2-i |
| 1 |
| 5 |
| 3 |
| 5 |
解答:解:∵
=
=
=
+
i,
=a+(b+1)i(a,b∈R),
∴
+
i=a+(b+1)i,
∴
,
∴复数z=a+bi=
-
i,
∴复数z=a+bi在复平面内对应的点的坐标为(
,-
),
故答案为 第四象限.
| 1+i |
| 2-i |
| (1+i)(2+i) |
| (2-i)(2+i) |
| 1+3i |
| 5 |
| 1 |
| 5 |
| 3 |
| 5 |
| 1+i |
| 2-i |
∴
| 1 |
| 5 |
| 3 |
| 5 |
∴
|
∴复数z=a+bi=
| 1 |
| 5 |
| 2 |
| 5 |
∴复数z=a+bi在复平面内对应的点的坐标为(
| 1 |
| 5 |
| 2 |
| 5 |
故答案为 第四象限.
点评:本题主要考查复数代数形式的混合运算,两个复数相等的充要条件,复数与复平面内对应点之间的关系,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
若i是虚数单位,设
=a+(b+1)i(a,b∈R),则复数Z=a+bi在复平面内对应的点位于( )
| 1+i |
| 2-i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
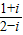 =a+(b+1)i(a,b∈R),则复数Z=a+bi在复平面内对应的点位于( )
=a+(b+1)i(a,b∈R),则复数Z=a+bi在复平面内对应的点位于( )