题目内容
以等腰直角△ABC的两个顶点为焦点,并且经过另一顶点的椭圆的离心率为( )
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
分析:分别以直角边和斜边为x轴,以直角边或斜边的垂直平分线为y轴,建立坐标系,再由题设条件求出椭圆方程,从而得到椭圆的离心率.
解答:解:在等腰直角三角形ABC中,∠ABC=90°,
若设BC=2,以BC为x轴,以BC的垂直平分线为y轴建立坐标系,
可知椭圆的焦点坐标是B(1,0),C(-1,0),且过点(1,2),
设椭圆方程是
+
=1,把(1,2)代入得
+
=1,解得a2=3+2
或a2=3-2
(舍去)
∴a=
+1或a=-
-1(舍去)
若设AC=2,以AC为x轴,以AC的垂直平分线为y轴建立坐标系,
可知椭圆的焦点坐标是C(1,0),A(-1,0),且过点(0,1),则c=1,b=1a=
,∴e=
.
故选C.
若设BC=2,以BC为x轴,以BC的垂直平分线为y轴建立坐标系,
可知椭圆的焦点坐标是B(1,0),C(-1,0),且过点(1,2),
设椭圆方程是
| x2 |
| a2 |
| y2 |
| a2-1 |
| 1 |
| a2 |
| 4 |
| a2-1 |
| 2 |
| 2 |
∴a=
| 2 |
| 2 |
若设AC=2,以AC为x轴,以AC的垂直平分线为y轴建立坐标系,
可知椭圆的焦点坐标是C(1,0),A(-1,0),且过点(0,1),则c=1,b=1a=
| 2 |
| ||
| 2 |
故选C.
点评:本题考查椭圆的性质及其应用,解题时要恰当地建立坐标系.

练习册系列答案
相关题目
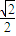
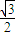
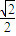 或
或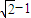
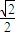 或
或