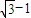题目内容
以等腰直角△ABC的两个顶点为焦点,且经过第三个顶点的双曲线的离心率为分析:根据题意△ABC为等腰直角三角形,设AB=2c,则AC=2c,BC=2
c,由双曲线的定义可得2
c-2c=2a,从而求得答案.
| 2 |
| 2 |
解答: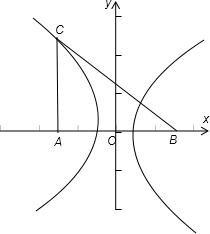 解:如图:△ABC为等腰直角三角形,
解:如图:△ABC为等腰直角三角形,
设AB=2c,则AC=2c,BC=2
c,
由双曲线的定义可得 2
c-2c=2a,
∴e=
=
=
+1,
故答案为
+1.
 解:如图:△ABC为等腰直角三角形,
解:如图:△ABC为等腰直角三角形,设AB=2c,则AC=2c,BC=2
| 2 |
由双曲线的定义可得 2
| 2 |
∴e=
| c |
| a |
| 1 | ||
|
| 2 |
故答案为
| 2 |
点评:本题考查双曲线的定义和标准方程,以及双曲线的简单性质的应用,体现了数形结合的数学思想,得到2
c-2c=2a,是解题的关键.
| 2 |

练习册系列答案
 培优三好生系列答案
培优三好生系列答案
相关题目
以等腰直角△ABC的两个顶点为焦点,并且经过另一顶点的椭圆的离心率为( )
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
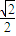
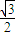
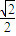 或
或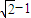
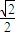 或
或