题目内容
已知偶函数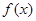 在区间
在区间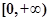 上单调增加,则
上单调增加,则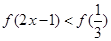 的x取值范围是( )
的x取值范围是( )


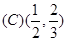
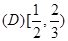
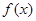 在区间
在区间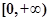 上单调增加,则
上单调增加,则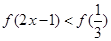 的x取值范围是( )
的x取值范围是( )

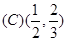
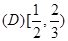
A
函数f(x)是偶函数,可得f(x)=f(|x|),利用偶函数f(x)在区间[0,+∞)上单调增加,满足f(2x-1)<f(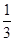 ),可得具体不等式,从而可求x取值范围.
),可得具体不等式,从而可求x取值范围.
解:∵函数f(x)是偶函数
∴f(x)=f(|x|)
∵偶函数f(x)在区间[0,+∞)上单调增加,满足f(2x-1)<f(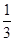 )
)
∴|2x-1|<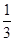
∴-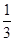 <2x-1<
<2x-1<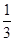
∴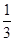 <x<
<x<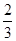
故选A.
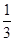 ),可得具体不等式,从而可求x取值范围.
),可得具体不等式,从而可求x取值范围.解:∵函数f(x)是偶函数
∴f(x)=f(|x|)
∵偶函数f(x)在区间[0,+∞)上单调增加,满足f(2x-1)<f(
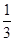 )
)∴|2x-1|<
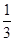
∴-
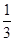 <2x-1<
<2x-1<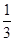
∴
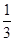 <x<
<x<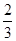
故选A.

练习册系列答案
相关题目
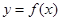 的反函数为
的反函数为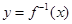 ,
,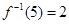 ,若函数
,若函数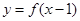 是
是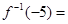 ( )
( )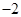
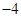
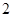
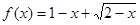 的值域为( )
的值域为( )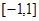
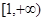
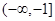
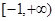

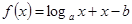
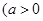 ,且
,且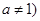 .当
.当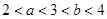 时,函数
时,函数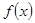 的零点
的零点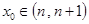 ,
,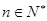 ,则
,则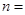 .
.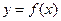 的图象关于直线
的图象关于直线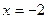 对称,当
对称,当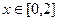 时,
时,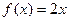 ,
, 则
则 = .
= .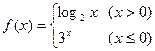 ,则
,则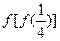 的值是
的值是 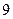
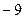
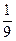
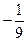
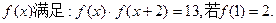 则
则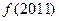 = .
= . (-1≤x<0)的反函数是
(-1≤x<0)的反函数是 (x≥
(x≥ )
)