题目内容
热力公司为某生活小区铺设暖气管道,为减少热量损耗,管道外表需要覆盖保温层,经测算要覆盖可使用20年的保温层,每厘米厚的保温层材料成本为2万元,小区每年的热量损耗费用w(单位:万元)与保温层厚度x(单位:cm)满足关系:w(x)=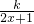 (0≤x≤10).若不加保温层,每年热量损耗费用5万元,设保温层费用与20年的热量损耗费用之和为f(x).
(0≤x≤10).若不加保温层,每年热量损耗费用5万元,设保温层费用与20年的热量损耗费用之和为f(x).
(1)求k的值及f(x)的表达式;
(2)问保温层多厚时,总费用f(x)最小,并求最小值.
解:(1)由题意知:W(0)=5,?K=5,?f(x)=2x+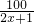 (0≤x≤10).
(0≤x≤10).
(2)∵f(x)=(2x+1)+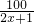 -1≥20-1=19,当且仅当2x+1=
-1≥20-1=19,当且仅当2x+1=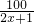 ,
,
即x=4.5时等号成立,
∴当保温层为4.5cm时,总费用最小且为19万元.
分析:(1)因为不加保温层,每年热量损耗费用5万元,所以将x=0时w=5代入w(x)求出参数k;求出保温层的费用为2x;求出20年的热量损耗费;将两者加起来为f(x)
(2)将f(x)中的2x写成(2x+1)-1,凑成乘积为定值;利用基本不等式求出f(x)的最小值,求出等号取到时对应的x的值.
点评:本题考查将实际问题转化为函数的最值问题、考查通过观察在函数中凑出定值,利用基本不等式求出最值.注意利用基本不等式求函数最值需注意满足的条件:一正、二定、三相等.
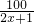 (0≤x≤10).
(0≤x≤10).(2)∵f(x)=(2x+1)+
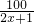 -1≥20-1=19,当且仅当2x+1=
-1≥20-1=19,当且仅当2x+1=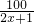 ,
,即x=4.5时等号成立,
∴当保温层为4.5cm时,总费用最小且为19万元.
分析:(1)因为不加保温层,每年热量损耗费用5万元,所以将x=0时w=5代入w(x)求出参数k;求出保温层的费用为2x;求出20年的热量损耗费;将两者加起来为f(x)
(2)将f(x)中的2x写成(2x+1)-1,凑成乘积为定值;利用基本不等式求出f(x)的最小值,求出等号取到时对应的x的值.
点评:本题考查将实际问题转化为函数的最值问题、考查通过观察在函数中凑出定值,利用基本不等式求出最值.注意利用基本不等式求函数最值需注意满足的条件:一正、二定、三相等.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
 (单位:万元)与保温层厚度
(单位:万元)与保温层厚度 (单位:
(单位: )满足关系:
)满足关系: 若不加保温层,每年热量损耗费用为5万元。设保温费用与20年的热量损耗费用之和为
若不加保温层,每年热量损耗费用为5万元。设保温费用与20年的热量损耗费用之和为
 的值及
的值及 的表达式;
的表达式; (0≤x≤10).若不加保温层,每年热量损耗费用5万元,设保温层费用与20年的热量损耗费用之和为f(x).
(0≤x≤10).若不加保温层,每年热量损耗费用5万元,设保温层费用与20年的热量损耗费用之和为f(x).