题目内容
已知点A(-1,0),点B (1,0),点P(x+1,y)在x轴的下方,设a=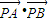 ,b=
,b=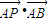 ,c=
,c=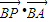 ,d=|
,d=|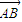 |,且
|,且 =0.
=0.(1)求a、b、c关于x、y的表达式;
(2)求y关于x的函数关系式y=f(x),并求当y取得最小值时P点的坐标.
【答案】分析:(1)因为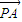 =(-x-2,-y),
=(-x-2,-y), =(-x,-y),
=(-x,-y),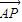 =(x+2,y),
=(x+2,y),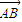 =(2,0),
=(2,0), =(x,y),
=(x,y),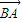 =(-2,0),由此能求出a、b、c关于x、y的表达式.
=(-2,0),由此能求出a、b、c关于x、y的表达式.
(2)因为 =0,所以3x2+y2+6x=0,由于点P(x+1,y)在x轴的下方,所以y=-
=0,所以3x2+y2+6x=0,由于点P(x+1,y)在x轴的下方,所以y=- ,(-2<x<0),y=-
,(-2<x<0),y=-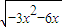 =-
=- ,(-2<x<0).由此能求出当y取得最小值时P点的坐标.
,(-2<x<0).由此能求出当y取得最小值时P点的坐标.
解答:解:(1)因为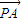 =(-x-2,-y),
=(-x-2,-y), =(-x,-y),
=(-x,-y),
所以a=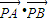 =x2+y2+2x,…(2分)
=x2+y2+2x,…(2分)
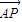 =(x+2,y),
=(x+2,y),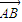 =(2,0),b=
=(2,0),b=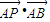 =2x+4,…(3分)
=2x+4,…(3分)
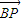 =(x,y),
=(x,y),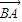 =(-2,0),c=
=(-2,0),c=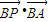 =-2x,…(4分)
=-2x,…(4分)
d= =2,…(5分)
=2,…(5分)
(2)因为 =0,所以2(x2+y2+2x)-(2x+4)(-2x)=0,即:3x2+y2+6x=0,…(7分)
=0,所以2(x2+y2+2x)-(2x+4)(-2x)=0,即:3x2+y2+6x=0,…(7分)
由于点P(x+1,y)在x轴的下方,所以y=-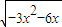 ,(-2<x<0)
,(-2<x<0)
y=-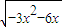 =-
=-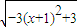 ,(-2<x<0)…(10分)
,(-2<x<0)…(10分)
所以当x=-1时,ymin=-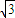 ,此时P(0,-
,此时P(0,-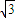 )…(12分)
)…(12分)
点评:本题考查矩阵现向量乘法的意义和应用,解题时要认真审题,注意平面向量的数量积公式的灵活运用.
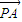 =(-x-2,-y),
=(-x-2,-y), =(-x,-y),
=(-x,-y),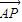 =(x+2,y),
=(x+2,y),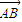 =(2,0),
=(2,0), =(x,y),
=(x,y),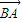 =(-2,0),由此能求出a、b、c关于x、y的表达式.
=(-2,0),由此能求出a、b、c关于x、y的表达式.(2)因为
 =0,所以3x2+y2+6x=0,由于点P(x+1,y)在x轴的下方,所以y=-
=0,所以3x2+y2+6x=0,由于点P(x+1,y)在x轴的下方,所以y=- ,(-2<x<0),y=-
,(-2<x<0),y=-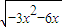 =-
=- ,(-2<x<0).由此能求出当y取得最小值时P点的坐标.
,(-2<x<0).由此能求出当y取得最小值时P点的坐标.解答:解:(1)因为
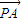 =(-x-2,-y),
=(-x-2,-y), =(-x,-y),
=(-x,-y),所以a=
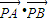 =x2+y2+2x,…(2分)
=x2+y2+2x,…(2分)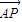 =(x+2,y),
=(x+2,y),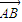 =(2,0),b=
=(2,0),b=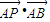 =2x+4,…(3分)
=2x+4,…(3分)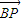 =(x,y),
=(x,y),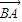 =(-2,0),c=
=(-2,0),c=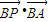 =-2x,…(4分)
=-2x,…(4分)d=
 =2,…(5分)
=2,…(5分)(2)因为
 =0,所以2(x2+y2+2x)-(2x+4)(-2x)=0,即:3x2+y2+6x=0,…(7分)
=0,所以2(x2+y2+2x)-(2x+4)(-2x)=0,即:3x2+y2+6x=0,…(7分)由于点P(x+1,y)在x轴的下方,所以y=-
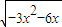 ,(-2<x<0)
,(-2<x<0)y=-
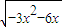 =-
=-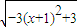 ,(-2<x<0)…(10分)
,(-2<x<0)…(10分)所以当x=-1时,ymin=-
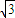 ,此时P(0,-
,此时P(0,-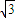 )…(12分)
)…(12分)点评:本题考查矩阵现向量乘法的意义和应用,解题时要认真审题,注意平面向量的数量积公式的灵活运用.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
 如图,已知点A(-1,0)与点B(1,0),C是圆x2+y2=1上的动点,连接BC并延长至D,使得|CD|=|BC|,求AC与OD的交点P的轨迹方程.
如图,已知点A(-1,0)与点B(1,0),C是圆x2+y2=1上的动点,连接BC并延长至D,使得|CD|=|BC|,求AC与OD的交点P的轨迹方程.