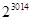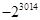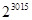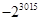题目内容
一份考卷有10道考题,分为A、B两组,每组5题,要求考生选答6题,但每组最多选4题,问考生有几种选答方式?
216
可分三类:A组选4题,B组选2题;A组选2题,B组选4题及A、B组各选3题.
故选答方法有2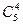
+
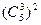=200种.
16.平面内有12个点，其中有4点共线，此外再无任何3点共线，以这些点为顶点可得到多少个不同的三角形？
分析1：该问题中三角形各顶点无顺序，是一个组合问题，我们考虑用直接法求解.
解法1：我们把从共线的4个点中取点的多少作为分类的标准.
第一类：共线的4点中有两点为三角形的顶点，共有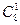
·
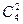=48（个）；
第二类：共线的4点中有一点为三角形的顶点，共有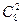
·
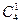=112（个）；
第三类：共线的4点中没有点作为三角形的项点，共有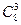
=56（个）.
由分类计数原理知，共有三角形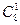·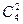+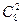·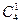+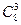=48+112+56=216（个）.
即可得到216个不同的三角形.
分析2：先看做无任何3点共线，再排除共线的4点算出三角形数目.
解法2：用排除法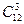
-
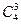=216（种）
故选答方法有2
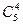
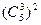+=200种.16.平面内有12个点，其中有4点共线，此外再无任何3点共线，以这些点为顶点可得到多少个不同的三角形？
分析1：该问题中三角形各顶点无顺序，是一个组合问题，我们考虑用直接法求解.
解法1：我们把从共线的4个点中取点的多少作为分类的标准.
第一类：共线的4点中有两点为三角形的顶点，共有
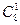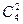·=48（个）；第二类：共线的4点中有一点为三角形的顶点，共有
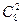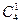·=112（个）；第三类：共线的4点中没有点作为三角形的项点，共有
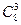=56（个）.由分类计数原理知，共有三角形
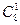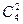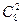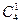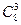·+·+=48+112+56=216（个）.即可得到216个不同的三角形.
分析2：先看做无任何3点共线，再排除共线的4点算出三角形数目.
解法2：用排除法
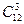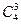-=216（种）
练习册系列答案
相关题目
个
种
种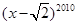
的二项展开式中，含
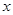的奇次幂的项之和为
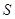，当
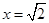时，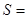
( )
