题目内容

若不等式a+2b+3＞(
a
+2
b
)λ对于任意正数a，b恒成立，则实数λ的取值范围为（　　）
A、(-∞，
1
2
)
B、（-∞，1）
C、（-∞，2）
D、（-∞，3）
分析：首先将不等式a+2b+3＞(
a
+2
b
)λ变形为λ＜
a+2b+3
a
+2
b
，利用a+2b+3=(a+1)+2(b+1)≥2 (
a
+2
b
)可求．
解答：解：由不等式a+2b+3＞(
a
+2
b
)λ可得λ＜
a+2b+3
a
+2
b
，由于a+2b+3=(a+1)+2(b+1)≥2 (
a
+2
b
)，∴λ＜2，
故选C．
点评：本题考查不等式的性质，基本不等式的应用，属于基础题
练习册系列答案
相关题目
本题有（1）、（2）、（3）三个选答题，每题7分，请考生任选2题作答，满分14分．如果多作，则按所做的前两题计分．作答时，先用2B铅笔在答题卡上把所选题目对应的题号涂黑，并将选题号填入括号中．
（1）选修4一2：矩阵与变换
求矩阵A=
2，1
3，0
的特征值及对应的特征向量．
（2）选修4一4：坐标系与参数方程
已知直线l的参数方程：
x=t
y=1+2t
（t为参数）和圆C的极坐标方程：ρ=2
2
sin(θ+
π
4
)．
（Ⅰ）将直线l的参数方程化为普通方程，圆C的极坐标方程化为直角坐标方程；
（Ⅱ）判断直线l和圆C的位置关系．
（3）选修4一5：不等式选讲
已知函数f（x）=|x-1|+|x-2|．若不等式|a+b|+|a-b|≥|a|f（x）（a≠0，a，b∈R）恒成立，求实数x的范围．
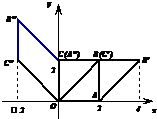精英家教网（Ⅰ）如图，正方形OABC在二阶矩阵M对应的切变变换作用下变为平行四边形OA′B′C′，平行四边形OA'B'C'在二阶矩阵N对应的旋转变换作用下变为平行四边形OA''B''C''，求将正方形OABC变为平行四边形OA''B''C''的变换对应的矩阵．
（Ⅱ）在直角坐标系xOy中，圆O的参数方程为
x=-
2
2
+rcosθ
y=-
2
2
+rsinθ
（θ为参数，r＞0）．以O为极点，x轴正半轴为极轴，并取相同的单位长度建立极坐标系，直线l的极坐标方程为ρsin(θ+
π
4
)=
2
2
．写出圆心的极标，并求当r为何值时，圆O上的点到直线l的最大距离为3．
（Ⅲ）已知a2+2b2+3c2=6，若存在实数a，b，c，使得不等式a+2b+3c＞|x+1|成立，求实数x的取值范围．

本题设有（1）（2）（3）三个选考题，每题7分，请考生任选2题作答，满分14分。如果多做，则按所做的前两题记分。作答时，先用2B铅笔在答题卡上把所选题目对应的题号涂黑，并将所选题号填入括号中。
（1）（本小题满分7分）选修4-2：矩阵与变换
已知矩阵M=，N=，且MN=。
（Ⅰ）求实数a,b,c,d的值；（Ⅱ）求直线y=3x在矩阵M所对应的线性变换作用下的像的方程。
（2）（本小题满分7分）选修4-4：坐标系与参数方程
在直角坐标系xOy中，直线L的参数方程为 （t为参数），在极坐标系（与直角坐标系xOy取相同的长度单位，且以原点O为极点，以x轴正半轴为极轴）中，圆C的方程为=2sin。
（Ⅰ）求圆C的直角坐标方程；
（Ⅱ）设圆C与直线L交于点A,B。若点P的坐标为（3，），求∣PA∣+∣PB∣。
（3）（本小题满分7分）选修4-5：不等式选讲
已知函数f(x)= ∣x-a∣.
（Ⅰ）若不等式f(x) 3的解集为，求实数a的值；
（Ⅱ）在（Ⅰ）的条件下，若f(x)+f(x+5)≥m对一切实数x恒成立，求实数m的取值范围。
本题有（1）、（2）、（3）三个选答题，每题7分，请考生任选2题作答，满分14分．如果多作，则按所做的前两题计分．作答时，先用2B铅笔在答题卡上把所选题目对应的题号涂黑，并将选题号填入括号中．
（1）选修4一2：矩阵与变换
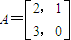求矩阵的特征值及对应的特征向量．
（2）选修4一4：坐标系与参数方程
已知直线l的参数方程：（t为参数）和圆C的极坐标方程：．
（Ⅰ）将直线l的参数方程化为普通方程，圆C的极坐标方程化为直角坐标方程；
（Ⅱ）判断直线l和圆C的位置关系．
（3）选修4一5：不等式选讲
已知函数f（x）=|x-1|+|x-2|．若不等式|a+b|+|a-b|≥|a|f（x）（a≠0，a，b∈R）恒成立，求实数x的范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网