题目内容
(2006年北京卷)已知函数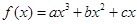 在点
在点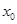 处取得极大值
处取得极大值 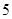 ,其导函数
,其导函数 的图象经过点
的图象经过点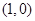 ,
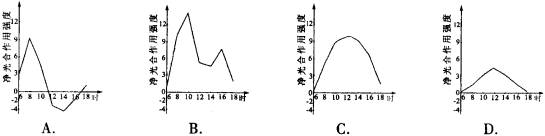
,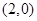 ,如图所示.求:
,如图所示.求:

(Ⅰ)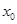 的值;
的值;
(Ⅱ)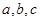 的值.
的值.
(Ⅰ) x0=1.(Ⅱ) a=2,b=-9,c=12
【解析】
试题分析:分析:根据导函数图像观察出函数的极大值,根据图像求出导函数
根据导函数和原函数的关系求解.
解:(Ⅰ)由图象可知,在(-∝,1)上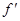 (x)>0,在(1,2)上
(x)>0,在(1,2)上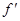 (x)<0.
(x)<0.
在(2,+∝)上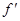 (x)>0.
(x)>0.
故f(x)在(-∝,1),(2,+∝)上递增,在(1,2)上递减.
因此f(x)在x=1处取得极大值,所以x0=1.
(Ⅱ) 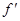 (x)=3ax2+2bx+c,
(x)=3ax2+2bx+c,
由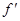 (1)=0,
(1)=0, 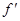 (2)=0, f(1)=5,
(2)=0, f(1)=5,
得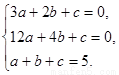 解得a=2,b=-9,c=12
解得a=2,b=-9,c=12
考点:本题主要考查导数在求函数的极值、研究函数单调性方面的应用。
点评:要注意三次函数及其导函数二次函数之间关系.

|