题目内容
已知O是锐角三角形ABC的外接圆的圆心，角A，B，C的对边分别为a，b，c，且A=
，若
•
+
•
=2m
，则m，的值为（ ）
| π |
| 4 |
| cosB |
| sinC |
| AB |
| cosC |
| sinB |
| AC |
| AO |
分析：根据三角形内心的充要条件：若O是锐角三角形ABC的外接圆的圆心，P是平面内任一点，则
=
+
+
，代入A=
，并令P与A点重合，可构造关于m的方程．
| PO |
| cosA |
| 2sinB•sinC |
| PA |
| cosB |
| 2sinA•sinC |
| PB |
| cosC |
| 2sinA•sinB |
| PC |
| π |
| 4 |
解答：解：∵O是锐角三角形ABC的外接圆的圆心，根据外心的充要条件可得，
对于平面内任意点P均有：
=
+
+
令P与A点重合，由A=
可得：
则
=
+
=
（
•
+
•
）
又∵
•
+
•
=2m
，
∴2m=
∴m=
故选A
对于平面内任意点P均有：
| PO |
| cosA |
| 2sinB•sinC |
| PA |
| cosB |
| 2sinA•sinC |
| PB |
| cosC |
| 2sinA•sinB |
| PC |
令P与A点重合，由A=
| π |
| 4 |
则
| AO |
| cosB | ||
|
| AB |
| cosC | ||
|
| AC |
| 2 |
| cosB |
| sinC |
| AB |
| cosC |
| sinB |
| AC |
又∵
| cosB |
| sinC |
| AB |
| cosC |
| sinB |
| AC |
| AO |
∴2m=
| 2 |
∴m=
| ||
| 2 |
故选A
点评：本题考查的知识点是向量在几何中的应用，其中熟练掌握三角形内心的充要条件：若O是锐角三角形ABC的外接圆的圆心，P是平面内任一点，则
=
+
+
，是解答的关键．
| PO |
| cosA |
| 2sinB•sinC |
| PA |
| cosB |
| 2sinA•sinC |
| PB |
| cosC |
| 2sinA•sinB |
| PC |
练习册系列答案
暑假作业海燕出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
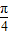，若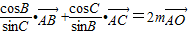
，则m，的值为（ ）
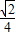
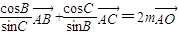，则m=（ ）