题目内容
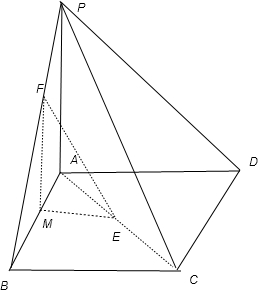
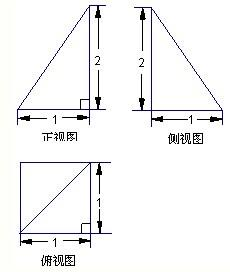
四棱锥P-ABCD的底面ABCD是正方形,E,F分别为AC和PB上的点,它的直观图,正视图,侧视图.如图所示,

(1)求EF与平面ABCD所成角的大小;
(2)求二面角B-PA-C的大小;
(3)求三棱锥C-BEF的体积.

(1)求EF与平面ABCD所成角的大小;
(2)求二面角B-PA-C的大小;
(3)求三棱锥C-BEF的体积.
分析:先由正视图及侧视图可得,四棱锥P-ABCD的底面ABCD是边长为4正方形,侧棱PA=4,且PA⊥平面ABCD
(1)由E,F为AC,PB的中点考虑取AB得中点M,则由已知可得MF⊥平面ABCD,则∠FEM即为直线EF与平面ABCD所成的角,在Rt△FEM中求解即可
(2)由已知条件可得,PA⊥AB,PA⊥AC可得∠BAC二面角B-PA-C的平面角
(3)由(1)知点F到平面BEC的距离为MF=2
由题意可得,利用换顶点求解VC-BEF=VF-BEC
(1)由E,F为AC,PB的中点考虑取AB得中点M,则由已知可得MF⊥平面ABCD,则∠FEM即为直线EF与平面ABCD所成的角,在Rt△FEM中求解即可
(2)由已知条件可得,PA⊥AB,PA⊥AC可得∠BAC二面角B-PA-C的平面角
(3)由(1)知点F到平面BEC的距离为MF=2
由题意可得,利用换顶点求解VC-BEF=VF-BEC
解答:解:由正视图及侧视图的可知,四棱锥P-ABCD的底面ABCD是边长为4正方形,侧棱PA=4,且PA⊥平面ABCD
(1)取AB得中点M,连接ME,MF
则可得MF∥PA,由PA⊥平面ABCD可得MF⊥平面ABCD
∴∠FEM即为直线EF与平面ABCD所成的角
在Rt△FEM中,FM=2,ME=2,∴∠FEM=45°
EF与平面ABCD所成角为45°
(2)由已知条件可得,PA⊥AB,PA⊥AC
∴∠BAC二面角B-PA-C的平面角
∵∠BAC=45°∴二面角B-PA-C的平面角的大小为45°
(3)由(1)知点F到平面BEC的距离为MF=2
由题意可得,VC-BEF=VF-BEC=
S△BEC•FM=
×
×4×2×2=
(1)取AB得中点M,连接ME,MF
则可得MF∥PA,由PA⊥平面ABCD可得MF⊥平面ABCD
∴∠FEM即为直线EF与平面ABCD所成的角
在Rt△FEM中,FM=2,ME=2,∴∠FEM=45°
EF与平面ABCD所成角为45°
(2)由已知条件可得,PA⊥AB,PA⊥AC
∴∠BAC二面角B-PA-C的平面角
∵∠BAC=45°∴二面角B-PA-C的平面角的大小为45°
(3)由(1)知点F到平面BEC的距离为MF=2
由题意可得,VC-BEF=VF-BEC=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 8 |
| 3 |

点评:本题主要考查了直线与平面所成的角及二面角的平面角的求解,其关键是要由三视图中的数据还原直观图的数据,而换顶点求解锥体的体积及求解点到直线的距离是高考的一个热点.

练习册系列答案
相关题目
 已知四棱锥P-ABCD的三视图如图所示,则这个四棱锥的体积为( )
已知四棱锥P-ABCD的三视图如图所示,则这个四棱锥的体积为( )A、
| ||
| B、1 | ||
C、
| ||
D、
|
 如图,四棱锥P-ABCD的底面是边长为1的正方形,侧棱PA⊥底面ABCD,且PA=2,E是PA的中点.
如图,四棱锥P-ABCD的底面是边长为1的正方形,侧棱PA⊥底面ABCD,且PA=2,E是PA的中点. 如图所示,四棱锥P-ABCD的底面是边长为a的正方形,侧棱PA⊥底面ABCD,侧面PBC内有BE⊥PC于E,且BE=
如图所示,四棱锥P-ABCD的底面是边长为a的正方形,侧棱PA⊥底面ABCD,侧面PBC内有BE⊥PC于E,且BE= 如图,ABCD是正方形,O是该正方形的中心,P是平面ABCD外一点,PO⊥底面ABCD,E是PC的中点.求证:
如图,ABCD是正方形,O是该正方形的中心,P是平面ABCD外一点,PO⊥底面ABCD,E是PC的中点.求证: