Question

【题目】已知椭圆的离心率为，点为椭圆上一点.

（1）求椭圆C的方程；

（2）已知两条互相垂直的直线，经过椭圆的右焦点，与椭圆交于四点，求四边形面积的的取值范围.

Answer 1

【答案】（1）；（2）

【解析】

（1）由题意可得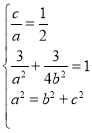，解得进而得到椭圆的方程；（2）设出直线l1，l2的方程，直线和椭圆方程联立，运用韦达定理和弦长公式，分别求得|AB|，|MN|，再由四边形的面积公式，化简整理计算即可得到取值范围．

（1）由题意可得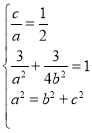，解得a2＝4，b2＝3，c2＝1

故椭圆C的方程为；

（2）当直线l1的方程为x＝1时，此时直线l2与x轴重合，

此时|AB|＝3，|MN|＝4，

∴四边形AMBN面积为S|AB||MN|＝6．

设过点F（1，0）作两条互相垂直的直线l1：x＝ky+1，直线l2：xy+1，

由x＝ky+1和椭圆1，可得（3k2+4）y2+6ky﹣9＝0，

判别式显然大于0，y1+y2，y1y2，

则|AB|，

把上式中的k换为，可得|MN|

则有四边形AMBN面积为S|AB||MN|，

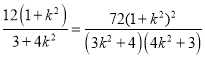令1+k2＝t，则3+4k2＝4t﹣1，3k2+4＝3t+1，

则S，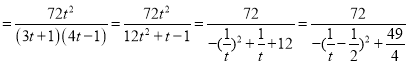

∴t＞1，

∴01，

∴y＝﹣（）2，在（0，）上单调递增，在（，1）上单调递减，

∴y∈（12，]，

∴S∈[，6）

故四边形PMQN面积的取值范围是