题目内容

三角形三边长之比为5：12：13，则此三角形为（　　）
A．锐角三角形B．直角三角形C．钝角三角形D．不存在
∵三角形三边长之比为5：12：13，
∴设△ABC的三边分别为a=5x，b=12x，c=13x．
∵a2+b2=169x2=c2，
∴由余弦定理，得cosC=
a2+b2-c2
2ab
=0，
结合0°＜C＜180°，得C=90°．
因此△ABC是以c为斜边的直角三角形．
故选：B
练习册系列答案
相关题目
设平面向量
m
=（cos2
x
2
，
3
sinx），
n
=（2，1），函数f（x）=
m
•
n
．
（Ⅰ）当x∈[-
π
3
，
π
2
]时，求函数f（x）的取值范围；
（Ⅱ）当f（α）=
13
5
，且-
2π
3
＜α＜
π
6
时，求sin（2α+
π
3
）的值．
直线l的倾斜角为θ，sinθ+cosθ=
7
13
，则斜率k的值为（　　）
A．-
12
5
B．
12
5
C．-
12
5
或-
5
12
D．-
5
12
已知△ABC满足c=2acosB，则△ABC的形状是（　　）
A．等腰三角形
B．直角三角形
C．等腰直角三角形
D．等腰三角形或直角三角形
若不等式a＞2sinxcosx+
3
cos2x恒成立，则实数a的取值范围为______．
已知函数f(x)=sinωx•cosωx+
3
cos2ωx-
3
2
（ω＞0），直线x=x1，x=x2是y=f（x）图象的任意两条对称轴，且|x1-x2|的最小值为
π
4
．
（I）求f（x）的表达式；
（Ⅱ）将函数f（x）的图象向右平移
π
8
个单位后，再将得到的图象上各点的横坐标伸长为原来的2倍，纵坐标不变，得到函数y=g（x）的图象，若关于x的方程g（x）+k=0，在区间[0，
π
2
]上有且只有一个实数解，求实数k的取值范围．
已知集合M={a，b，c}中的三个元素可构成某一三角形的三边长，那么此三角形一定不是（　　）
A．直角三角形B．锐角三角形C．等腰三角形D．钝角三角形
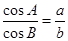在△ABC中，已知，则△ABC的形状为          .
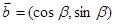已知向量 ，下列结论中正确的是（ ）
A．B．
C．D．、的夹角为

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网