题目内容
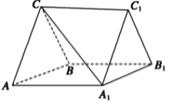
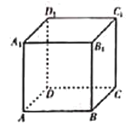
【题目】如图,关于正方体![]() ,有下列四个命题:
,有下列四个命题:
①![]() 与平面
与平面![]() 所成角为45°;
所成角为45°;
②三棱锥![]() 与三棱锥
与三棱锥![]() 的体积比为
的体积比为![]() ;
;
③存在唯一平面![]() .使
.使![]() 平面
平面![]() 且
且![]() 截此正方体所得截面为正六边形;
截此正方体所得截面为正六边形;
④过![]() 作平面
作平面![]() ,使得棱
,使得棱![]() 、
、![]() ,
,![]() 在平面
在平面![]() 上的正投影的长度相等.则这样的平面
上的正投影的长度相等.则这样的平面![]() 有且仅有一个.
有且仅有一个.
上述四个命题中,正确命题的序号为________.
【答案】①②③.
【解析】
根据线面角的求解方法,三棱锥体积计算公式,正方体截面的性质,以及投影的相关知识,对选项进行逐一分析即可.
对①:过![]() 作
作![]() 垂直于
垂直于![]() ,垂足为
,垂足为![]() ,如下图所示:
,如下图所示:
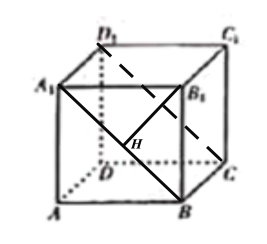
因为![]() 是正方体,
是正方体,
容易知![]() 平面
平面![]() ,且
,且![]() 平面
平面![]() ,故可得
,故可得![]() ,
,
又因为![]() ,故
,故![]() 平面
平面![]() ,故
,故![]() 即为所求线面角.
即为所求线面角.
容易知![]() 为等腰直角三角形,故
为等腰直角三角形,故![]() .
.
即![]() 与平面
与平面![]() 所成角为45°.故①正确;
所成角为45°.故①正确;
对②:设正方体棱长为1,
故可得![]() ;
;
而棱锥![]() 的体积可以理解为
的体积可以理解为
正方体的体积减去4个体积都和![]() 相等的三棱锥的体积,
相等的三棱锥的体积,
故![]() .
.
故棱锥![]() 与三棱锥
与三棱锥![]() 的体积比为
的体积比为![]() ,则②正确;
,则②正确;
对③:根据正方体截面的性质,当截面为六边形时,
当且仅当![]() 为各点所在棱的中点时,截面为正六边形,如下图所示:
为各点所在棱的中点时,截面为正六边形,如下图所示:
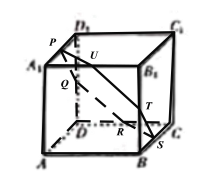
其它情况下,无法保证截面六边形的棱长都相等,
故存在唯一平面![]() .使
.使![]() 平面
平面![]() 且
且![]() 截此正方体所得截面为正六边形,
截此正方体所得截面为正六边形,
则③正确;
对④:若棱![]() 在平面
在平面![]() 的同侧,则
的同侧,则![]() 为过点
为过点![]() 且与平面
且与平面![]() 平行的平面;
平行的平面;
若棱![]() 中有一条棱与另外两条棱分别在平面
中有一条棱与另外两条棱分别在平面![]() 的异侧,则这样的平面有3个;
的异侧,则这样的平面有3个;
故满足题意的平面![]() 有4个.
有4个.
故④错误.
综上所述:正确的有①②③.
故答案为:①②③.

练习册系列答案
相关题目