题目内容
已知函数f(x)=x3-ax2+bx+c的图象为曲线E.
(1)若函数f(x)在x=-1和x=3时取得极值,求a、b的值;
(2)若曲线E上存在点P,使曲线E在P点处的切线与x轴平行,求a、b满足的关系式;
(3)在(1)的条件下,当x∈[-2,6]时,f(x)<2|c|恒成立,求c的取值范围.
答案:
解析:
解析:
|
解析:(1) ∵f(x)在x=-1,3时存在极值, ∴-1、3是方程3x2-2ax+b=0的两实数根. ∴ (2)∵曲线E上存在与x轴平行的切线, ∴ ∴Δ=(-2a)2-12b≥0. ∴a、b的关系式为a2≥3b. (3)f(x)=x3-3x2-9x+c, 当x变化时,
x∈[-2,6]时,f(x)的最大值为c+54, 要使f(x)<2|c|恒成立,只需c+54<2|c|, c≥0时,c+54<2c, ∴c>54;c<0时,c+54<-2c. ∴c<-18. ∴c的范围是(-∞,-18)∪(54,+∞). |

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案
相关题目
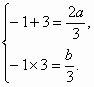 ∴
∴ g(x)恒成立,求实数a的取值范围.
g(x)恒成立,求实数a的取值范围. x3+
x3+ x2-ax-a,x∈R,其中a>0.
x2-ax-a,x∈R,其中a>0. ax2+3x.
ax2+3x.