题目内容
将集合M={1,2,…12}的元素分成不相交的三个子集:M=A∪B∪C,其中A={a1,a2,a3,a4}B={b1,b2,b3,b4}C={c1,c2,c3,c4},c1<c2<c3<c4,且ak+bk=ck,k=1,2,3,4,则集合C为:
{8,9,10,12},{7,9,11,12},{6,10,11,12}
{8,9,10,12},{7,9,11,12},{6,10,11,12}
.分析:由
ci=
ai+
bi,得2
ci=
ai+
bi+
ci=1+2+…+12=78,所以
ci=39,由此入手能够求出集合C.
| 4 |
 |
| i=1 |
| 4 |
 |
| i=1 |
| 4 |
 |
| i=1 |
| 4 |
 |
| i=1 |
| 4 |
 |
| i=1 |
| 4 |
 |
| i=1 |
| 4 |
 |
| i=1 |
| 4 |
 |
| i=1 |
解答:解:由
ci=
ai+
bi,
得2
ci=
ai+
bi+
ci=1+2+…+12=78,
所以
ci=39,
先不考虑搭配情况,设c1<c2<c3<c4,则c4=12,c1+c2+c3=27,
故3c3>27,10≤c3≤11,且c2≤9;
若c3=10,则c1+c2=17,c2≥9,所以c2=9,c1=8;
于是C={8,9,10,12};
若c3=11,则c1+c2=16,c2≤10,得c2>8,
故c2只能取9或10,c1只能取7与6;
分别得C={7,9,11,12},C={6,10,11,12};
另一方面,三种情况都对应有相应的子集A和B,例如以下的表:
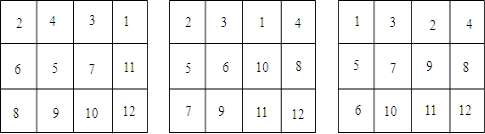
因此子集C的三种情况都合条件.
故答案为::{8,9,10,12},{7,9,11,12},{6,10,11,12}.
| 4 |
 |
| i=1 |
| 4 |
 |
| i=1 |
| 4 |
 |
| i=1 |
得2
| 4 |
 |
| i=1 |
| 4 |
 |
| i=1 |
| 4 |
 |
| i=1 |
| 4 |
 |
| i=1 |
所以
| 4 |
 |
| i=1 |
先不考虑搭配情况,设c1<c2<c3<c4,则c4=12,c1+c2+c3=27,
故3c3>27,10≤c3≤11,且c2≤9;
若c3=10,则c1+c2=17,c2≥9,所以c2=9,c1=8;
于是C={8,9,10,12};
若c3=11,则c1+c2=16,c2≤10,得c2>8,
故c2只能取9或10,c1只能取7与6;
分别得C={7,9,11,12},C={6,10,11,12};
另一方面,三种情况都对应有相应的子集A和B,例如以下的表:

因此子集C的三种情况都合条件.
故答案为::{8,9,10,12},{7,9,11,12},{6,10,11,12}.
点评:本题考查集合的交、并、补的混合运算,是中档题.解题时要认真审题,仔细解答,注意合理地进行等价转化.

练习册系列答案
相关题目