题目内容
记集合A={1,2,3,4,5,6},M={m|m=
+
+
,a1,a2,a3∈A},将M中的元素按从小到大的顺序排列,则第70个元素是( )
| a1 |
| 10 |
| a2 |
| 102 |
| a3 |
| 103 |
分析:根据题意,由乘法原理分析可得当a1=1时,m可取的值有36个,是M中前36个元素,同理可得当a1=2时,m可取的值也有36个,进而分析当a1=2时,M中最大的元素,即第72个元素,第71个元素,第70个元素,即可得答案.
解答:解:根据题意,a1、a2、a3∈A,则a1、a2、a3都有6种情况,
则m的值可有6×6×6=216,故M中有216个元素,
当a1=1时,a2、a3有6×6=36种情况,此时m的值有36个,是M中前36个元素,
当a1=2时,a2、a3有6×6=36种情况,此时m的值有36个,是M中第37到72个元素,
其中最大的数为0.266,即M中第72个元素,
其第71个元素0.265,
第70个元素为0.264,
故选A.
则m的值可有6×6×6=216,故M中有216个元素,
当a1=1时,a2、a3有6×6=36种情况,此时m的值有36个,是M中前36个元素,
当a1=2时,a2、a3有6×6=36种情况,此时m的值有36个,是M中第37到72个元素,
其中最大的数为0.266,即M中第72个元素,
其第71个元素0.265,
第70个元素为0.264,
故选A.
点评:本题考查排列、组合的应用,关键是求出M中第70个元素,要注意a1、a2、a3可以相同.

练习册系列答案
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案
相关题目
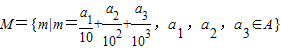 ,将M中的元素按从小到大的顺序排列,则第70个元素是( )
,将M中的元素按从小到大的顺序排列,则第70个元素是( )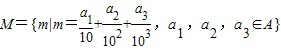 ,将M中的元素按从小到大的顺序排列,则第70个元素是( )
,将M中的元素按从小到大的顺序排列,则第70个元素是( )