题目内容
16.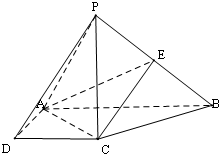 如图,在四棱锥P-ABCD中,PC⊥底面ABCD,底面ABCD是直角梯形,AB⊥AD,AB∥CD,AB=2AD=2CD=2,PC<2,E是PB的中点.
如图,在四棱锥P-ABCD中,PC⊥底面ABCD,底面ABCD是直角梯形,AB⊥AD,AB∥CD,AB=2AD=2CD=2,PC<2,E是PB的中点.(1)求证:平面EAC⊥平面PBC;
(2)若直线PA与平面EAC所成角的正弦值为$\frac{\sqrt{2}}{3}$,求平面PAC与平面ACE夹角的余弦值.
分析 (1)由题意可得AC⊥PC,再由勾股定理可得AC⊥BC,可得AC⊥平面PBC,进而可判平面EAC平面PBC;
(2)以C为原点,建立空间直角坐标系如图所示,分别可得平面PAC和EAC的法向量,待定系数可得a值,由向量的夹角公式可得答案.
解答 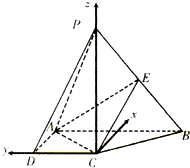 解:(1)∵PC⊥平面ABCD,AC?平面ABCD,∴AC⊥PC,
解:(1)∵PC⊥平面ABCD,AC?平面ABCD,∴AC⊥PC,
∵AB=2,AD=CD=1,∴AC=BC=$\sqrt{2}$,
∴AC2+BC2=AB2,∴AC⊥BC,
又BC∩PC=C,∴AC⊥平面PBC,
∵AC?平面EAC,∴平面EAC平面PBC;
(2)以C为原点,建立空间直角坐标系如图所示,
则C(0,0,0),A(1,1,0),B(1,-1,0),
设P(0,0,a)(a>0),则E($\frac{1}{2}$,-$\frac{1}{2}$,$\frac{a}{2}$),
∴$\overrightarrow{CA}$=(1,1,0),$\overrightarrow{CP}$=(0,0,a)(a>0),
$\overrightarrow{CE}$=($\frac{1}{2}$,-$\frac{1}{2}$,$\frac{a}{2}$),$\overrightarrow{PA}$=(1,1,-a),
设$\overrightarrow{m}$=(x,y,z)为平面PAC的法向量,
则$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{CP}=az=0}\\{\overrightarrow{m}•\overrightarrow{CA}=x+y=0}\end{array}\right.$,可取$\overrightarrow{m}$=(1,-1,0)
同理平面EAC的法向量$\overrightarrow{n}$=(a,-a,-2),
依题意,设直线PA与平面EAC所成角为θ,
则sinθ=|cos<$\overrightarrow{PA}$,$\overrightarrow{n}$>|=$\frac{2a}{\sqrt{{a}^{2}+2}•\sqrt{2{a}^{2}+4}}$=$\frac{\sqrt{2}}{3}$,
解得a=1,或a=2(舍去,此时不满足PC<2),
∴$\overrightarrow{n}$=(1,-1,-2),
∴|cos<$\overrightarrow{m}$,$\overrightarrow{n}$>|=$\frac{|\overrightarrow{m}•\overrightarrow{n}|}{|\overrightarrow{m}||\overrightarrow{n}|}$=$\frac{\sqrt{3}}{3}$
∴平面PAC与平面ACE夹角的余弦值为$\frac{\sqrt{3}}{3}$
点评 本题考查空间向量法解决立体几何问题,涉及平面与平面垂直的判定,属中档题.

| A. | f(x)为偶函数 | B. | f(x)在[-$\frac{π}{2}$,$\frac{π}{2}$]上单调递增 | ||
| C. | x=$\frac{π}{2}$为f(x)的图象的一条对称轴 | D. | ($\frac{π}{2}$,0)为f(x)的图象的一个对称中心 |
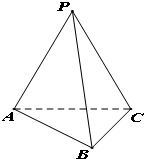 如图,在三棱锥P-ABC中,平面APC⊥平面ABC,且PA=PB=PC=4,AB=BC=2.
如图,在三棱锥P-ABC中,平面APC⊥平面ABC,且PA=PB=PC=4,AB=BC=2.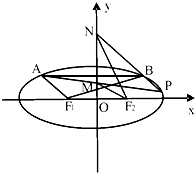 如图,F1,F2分别是椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点,且焦距为2$\sqrt{2}$,动弦AB平行于x轴,且|F1A|+|F2A|=4.
如图,F1,F2分别是椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点,且焦距为2$\sqrt{2}$,动弦AB平行于x轴,且|F1A|+|F2A|=4. ,则函数
,则函数 与函数
与函数 的图象交点的个数为( )
的图象交点的个数为( )