题目内容
16.某工厂统计资料显示,该厂生产的某种产品次品率p与日产量x(千克)(x∈N,且11≤x≤100)的关系如表,| x | 11 | 12 | 13 | 14 | … | 99 | 100 |
| p | $\frac{2}{97}$ | $\frac{1}{48}$ | $\frac{2}{95}$ | $\frac{1}{47}$ | … | $\frac{1}{9}$ | $\frac{1}{4}$ |
(1)写出生产该产品的日盈利额T(元)表示为日产量x的一个函数关系式;
(2)为了获得最大盈利,该厂生产该产品的日产量应定为多少千克?
分析 (1)根据表格,先确定p=$\frac{2}{108-x}$,x中次品有xp,正品有(x-xp),进而可得该厂日盈利额T关于日产量x的函数;
(2)利用基本不等式可确定函数的最值.
解答 解:(1)由题意知 p=$\frac{2}{108-x}$,x中次品有xp,正品有(x-xp)
所以该厂日盈利额T=a(x-xp)-$\frac{a}{2}$xp=a(x-$\frac{3p}{2}$x)=a(x-$\frac{3x}{108-x}$),(11≤x≤100,x∈N*)
(2)T=a(x-$\frac{3x}{108-x}$)=a[x-$\frac{3(x-108)+324}{108-x}$]=a(x+3-$\frac{324}{108-x}$)
=a(x-108+105-$\frac{324}{108-x}$)
=a[-(108-x)-$\frac{324}{108-x}$)+105]≤a[105+2$\sqrt{-(108-x)•(-\frac{324}{108-x}})$]=a(105+36)=141a
当且仅当-(108-x)=-$\frac{324}{108-x}$),即x=90,取等号
∵11≤x≤100,
∴x=90时,该厂盈利最大.
即为了获得最大盈利,该厂生产该产品的日产量应定为90千克.
点评 本题考查函数模型的构建,考查利用基本不等式求函数的最值,确定函数模型是关键.

练习册系列答案
相关题目
11.函数y=$\frac{1}{\sqrt{x-{x}^{2}}}$的最小值为( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | 2 | D. | 4 |
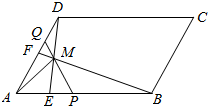 如图所示,在平行四边形ABCD中,$\overrightarrow{AE}$=$\frac{1}{4}$$\overrightarrow{AB}$,$\overrightarrow{AF}$=$\frac{1}{2}$$\overrightarrow{AD}$,BF与DE交于点M,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$.
如图所示,在平行四边形ABCD中,$\overrightarrow{AE}$=$\frac{1}{4}$$\overrightarrow{AB}$,$\overrightarrow{AF}$=$\frac{1}{2}$$\overrightarrow{AD}$,BF与DE交于点M,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$.