题目内容
已知椭圆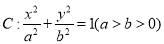 经过点
经过点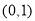 ,离心率为
,离心率为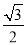 .
.
(1)求椭圆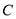 的方程;
的方程;
(2)设直线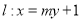 与椭圆
与椭圆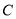 交于
交于 ,点
,点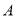 关于
关于 轴的对称点
轴的对称点 (
(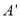 与
与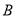 不重合),则直线
不重合),则直线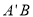 与
与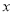 轴是否交于一定点?若是,请写出定点坐标,并证明你的结论;若不是,请说明理由.
轴是否交于一定点?若是,请写出定点坐标,并证明你的结论;若不是,请说明理由.
练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
题目内容
已知椭圆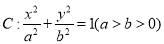 经过点
经过点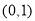 ,离心率为
,离心率为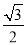 .
.
(1)求椭圆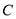 的方程;
的方程;
(2)设直线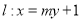 与椭圆
与椭圆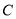 交于
交于 ,点
,点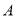 关于
关于 轴的对称点
轴的对称点 (
(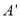 与
与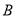 不重合),则直线
不重合),则直线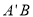 与
与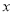 轴是否交于一定点?若是,请写出定点坐标,并证明你的结论;若不是,请说明理由.
轴是否交于一定点?若是,请写出定点坐标,并证明你的结论;若不是,请说明理由.
 高中必刷题系列答案
高中必刷题系列答案