题目内容
已知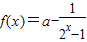 是定义在(-∞,-1]∪[1,+∞)上的奇函数,则f(x)的值域为 .
是定义在(-∞,-1]∪[1,+∞)上的奇函数,则f(x)的值域为 .
【答案】分析:根据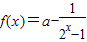 是奇函数,可确定a的值,进而可得函数的解析式,利用函数的定义域,可确定函数的值域.
是奇函数,可确定a的值,进而可得函数的解析式,利用函数的定义域,可确定函数的值域.
解答:解:∵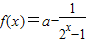 是定义在(-∞,-1]∪[1,+∞)上的奇函数
是定义在(-∞,-1]∪[1,+∞)上的奇函数
∴f(-x)=-f(x)
∴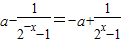
∴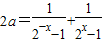
∴
∴2a=-1,∴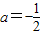
∴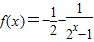
∵x∈(-∞,-1]∪[1,+∞)
∴2x∈(0, ]∪[2,+∞)
]∪[2,+∞)
∴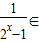 [-2,-1)∪(0,1]
[-2,-1)∪(0,1]
∴f(x)∈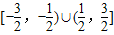
故答案为: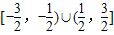
点评:本题重点考查函数的奇偶性,考查函数的值域,解题的关键是确定函数的解析式,属于基础题.
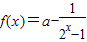 是奇函数,可确定a的值,进而可得函数的解析式,利用函数的定义域,可确定函数的值域.
是奇函数,可确定a的值,进而可得函数的解析式,利用函数的定义域,可确定函数的值域.解答:解:∵
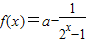 是定义在(-∞,-1]∪[1,+∞)上的奇函数
是定义在(-∞,-1]∪[1,+∞)上的奇函数∴f(-x)=-f(x)
∴
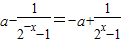
∴
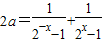
∴

∴2a=-1,∴
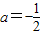
∴
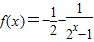
∵x∈(-∞,-1]∪[1,+∞)
∴2x∈(0,
 ]∪[2,+∞)
]∪[2,+∞)∴
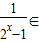 [-2,-1)∪(0,1]
[-2,-1)∪(0,1]∴f(x)∈
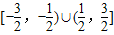
故答案为:
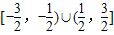
点评:本题重点考查函数的奇偶性,考查函数的值域,解题的关键是确定函数的解析式,属于基础题.

练习册系列答案
相关题目
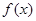 是定义在R上的偶函数,对任意
是定义在R上的偶函数,对任意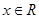 ,都有
,都有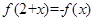 ,且当
,且当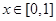 时在
时在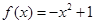 ,若
,若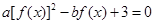 在
在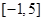 上有5个根
上有5个根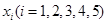 ,则
,则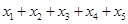 的值为( )
的值为( )