题目内容
函数 在[0,1]上是
在[0,1]上是 的减函数,则
的减函数,则 的取值范围是( )
的取值范围是( )
| A.(0,1) | B.(0,2) | C.(1,2) | D.[2,+ ) ) |
C
解析试题分析:∵a>0,∴2-ax在[0,1]上是减函数.
∴y=logau应为增函数,且u=2-ax在[0,1]上应恒大于零.
∴a>1,2-a>0,∴1<a<2,故答案为:C.
考点:本试题主要考查了对数函数单调性的运用。
点评:解决该试题的关键是对数函数与其它函数复合在一起的一新函数的单调性,复合函数的单调性遵循的原则是同增异减,即单调性相同复合在一起为增函数,单调性相反,复合在一起为减函数。

练习册系列答案
相关题目
 恒过定点( )
恒过定点( )
A. | B.  | C. | D.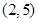 |
下列函数中,在(0,2)上为增函数的是( )
A.y=log (x+1) (x+1) | B.y=log2 |
C.y=log2 | D.y=log (x2-4x+5) (x2-4x+5) |
已知 是奇函数,且在
是奇函数,且在 是增函数,又
是增函数,又 ,则
,则 < 0的解集是( )
< 0的解集是( )
A. | B. |
C. | D. |
已知 ,
, ,
, ,则
,则 的大小关系是
的大小关系是
A. | B. |
C.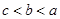 | D. |
某人 年
年 月
月 日到银行存入一年期存款
日到银行存入一年期存款 元,若按年利率为
元,若按年利率为 ,并按复利计算,到
,并按复利计算,到 年
年 月
月 日可取回的款共( )
日可取回的款共( )
A. 元 元 | B. 元 元 | C. 元 元 | D. 元 元 |
设偶函数f(x)的定义域为R,当x 时f(x)是增函数,则f(-2),f(
时f(x)是增函数,则f(-2),f( ),f(-3)的大小关系是( )
),f(-3)的大小关系是( )
A.f( )>f(-3)>f(-2) )>f(-3)>f(-2) | B.f( )>f(-2)>f(-3) )>f(-2)>f(-3) |
C.f( )<f(-3)<f(-2) )<f(-3)<f(-2) | D.f( )<f(-2)<f(-3) )<f(-2)<f(-3) |
当 时,在同一坐标系中,函数
时,在同一坐标系中,函数 的图象是( )
的图象是( )
A. | B. |
C.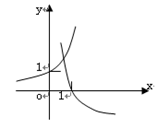 | D. |
 的图象可能是( ).
的图象可能是( ).