题目内容
 恒过定点( )
恒过定点( )
A. | B.  | C. | D.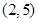 |
D
解析试题分析:因为对数函数恒过点(1,0),那么可知令x-1=1,得到 =0,即x=2,此时y=5,则说明函数
=0,即x=2,此时y=5,则说明函数 恒过点(1,5),因此答案为
恒过点(1,5),因此答案为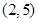 ,故选D.
,故选D.
考点:本题主要考查对数函数的性质的运用。
点评:解决该试题的关键是理解对数函数恒过定点(1,0)的真正含义,就是让对数的真数为零,无论底数是多少,则函数值始终为0。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
三个数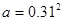 ,
, ,
, 之间的大小关系为( )
之间的大小关系为( )
| A.a<c<b | B.a<b<c | C.b<a<c | D.b<c<a |
已知函数 ,则
,则 ( )
( )
| A.16 | B.8 | C.-8 | D.8或-8 |
已知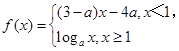 是(-
是(-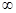 ,+
,+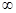 )上的增函数,那么
)上的增函数,那么 的取值范围是( )
的取值范围是( )
A.(1, +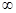 ) ) | B.(-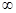 ,3) ,3) | C.[ ,3) ,3) | D.(1,3) |
函数 在区间
在区间 上的最大值与最小值的和为3,则
上的最大值与最小值的和为3,则 等于( )
等于( )
A. | B.4 | C.2 | D. |
函数 的图象必过定点( )
的图象必过定点( )
A. | B. | C. | D. |
函数 在[0,1]上是
在[0,1]上是 的减函数,则
的减函数,则 的取值范围是( )
的取值范围是( )
| A.(0,1) | B.(0,2) | C.(1,2) | D.[2,+ ) ) |
 与
与 在同一坐标系中的图像只可能是
在同一坐标系中的图像只可能是
 的图像大致形状是( )
的图像大致形状是( )