题目内容
设a>1,且m=loga(a2+1),n=loga(a-1),p=loga(2a),则m,n,p的
大小关系为
大小关系为
| A.n>m>p | B.m>p>n | C.m>n>p | D.p>m>n |
B
分析:因为0<a<1时,y=logax为减函数,故只需比较a2+1、a+1、2a的大小.可用特值取a=2.
解答:解:取a=2,则a2+1、2a、 a-1的大小分别为:5,4,1又因为a>1时,y=logax为增函数,所以m>p>n
故选B
解答:解:取a=2,则a2+1、2a、 a-1的大小分别为:5,4,1又因为a>1时,y=logax为增函数,所以m>p>n
故选B

练习册系列答案
相关题目

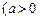 且
且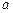 ≠1)
≠1)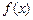 的单调性。(12分)
的单调性。(12分)
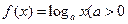 且
且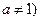 在区间[,4]上的最大值与最小值的差为3,求
在区间[,4]上的最大值与最小值的差为3,求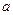 .
.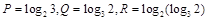 ,则()
,则()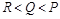

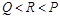
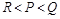
 x2-ax+3a)在[2, +∞)是增函数,则实数a的取值范围是 .
x2-ax+3a)在[2, +∞)是增函数,则实数a的取值范围是 . 




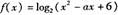 在
在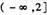 上是减函数,则实数a的取值范围是
上是减函数,则实数a的取值范围是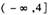 b.
b.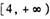 c.
c.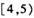 d.
d.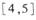
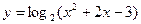 的单调增区间是 ;
的单调增区间是 ;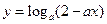 在[0,1]上是
在[0,1]上是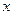 的减函数,则
的减函数,则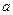 的取值范围是 ( )
的取值范围是 ( )