题目内容
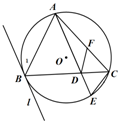
（2013•兰州一模）选修4-1：《几何证明选讲》已知：如图，eO为△ABC的外接圆，直线l为eO的切线，切点为B，直线AD∥l，交BC于D、交eO于E，F为AC上一点，且∠EDC=∠FDC．求证：
（Ⅰ）AB2=BD．BC；
（Ⅱ）点A、B、D、F共圆．
分析：（I）欲证AB2=BD•BC，即证
=
，只须证△ABC∽△DAB．根据相似三角形的判定，由于∠ABC=∠DBA，只须证明∠ACB=∠DAB即可．
（II）要证明A、B、D、F四点共圆，根据四点共圆定理只要证∠BAC+∠EDC=180°即可．
| AB |
| DB |
| BC |
| AB |
（II）要证明A、B、D、F四点共圆，根据四点共圆定理只要证∠BAC+∠EDC=180°即可．
解答：证明：（1）∵直线l为圆O的切线，∴∠1=∠ACB．
∵AD∥l，∴∠1=∠DAB．
∴∠ACB=∠DAB，
又∵∠ABC=∠DBA，
∴△ABC∽△DAB．
∴
=
．
∴AB2=BD•BC．…（5分）
（Ⅱ）由（Ⅰ）可知∠BAC=∠ADB．
∵∠EDC=∠FDC，∠EDC=∠ADB，
∴∠BAC=∠FDC．∴∠BAC+∠EDC=∠FDC+∠FDB=180°．
∴点A、B、D、F共圆．…（10分）
∵AD∥l，∴∠1=∠DAB．∴∠ACB=∠DAB，
又∵∠ABC=∠DBA，
∴△ABC∽△DAB．
∴
| AB |
| DB |
| BC |
| AB |
∴AB2=BD•BC．…（5分）
（Ⅱ）由（Ⅰ）可知∠BAC=∠ADB．
∵∠EDC=∠FDC，∠EDC=∠ADB，
∴∠BAC=∠FDC．∴∠BAC+∠EDC=∠FDC+∠FDB=180°．
∴点A、B、D、F共圆．…（10分）
点评：本题考查与圆有关的比例线段的应用，是基础题．解题时要认真审题，仔细解答，注意合理地进行等价转化．
练习册系列答案
步步高口算题卡系列答案
点睛新教材全能解读系列答案
小学教材完全解读系列答案
相关题目