题目内容
(本小题满分13分)
已知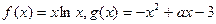 .
.
(I)求函数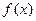 在
在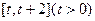 上的最小值;
上的最小值;
(II)对一切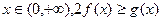 恒成立,求实数
恒成立,求实数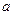 的取值范围.
的取值范围.
已知
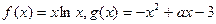 .
.(I)求函数
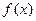 在
在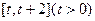 上的最小值;
上的最小值;(II)对一切
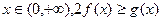 恒成立,求实数
恒成立,求实数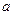 的取值范围.
的取值范围.解:(1)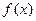 定义域为
定义域为 ,
,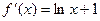 ,
,
当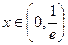 ,
,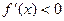 ,
,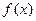 单调递减,
单调递减,
当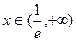 ,
,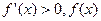 单调递增. ……………………………………2分
单调递增. ……………………………………2分
①当 无解;……………………………………………………………3分
无解;……………………………………………………………3分
②当 ,即
,即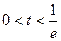 时,
时,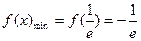 ; …………4分
; …………4分
③当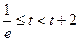 即
即 时,
时,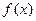 在
在 上单调递增,
上单调递增, ;
;
………5分
所以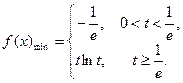 ………6分
………6分
(2) ,则
,则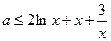 ,对一切
,对一切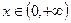 恒成立.……7分
恒成立.……7分
设 ,则
,则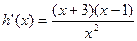 ,
,
当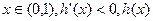 单调递减,
单调递减,
当 单调递增. …………10分
单调递增. …………10分
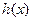 在
在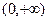 上,有唯一极小值
上,有唯一极小值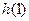 ,即为最小值.
,即为最小值.
所以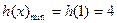 ,因为对一切
,因为对一切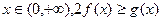 恒成成立,
恒成成立,
所以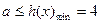 . ……………………………13分
. ……………………………13分
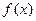 定义域为
定义域为 ,
,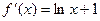 ,
,当
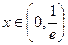 ,
,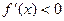 ,
,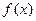 单调递减,
单调递减,当
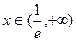 ,
,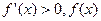 单调递增. ……………………………………2分
单调递增. ……………………………………2分①当
 无解;……………………………………………………………3分
无解;……………………………………………………………3分②当
 ,即
,即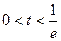 时,
时,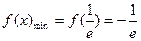 ; …………4分
; …………4分③当
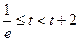 即
即 时,
时,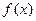 在
在 上单调递增,
上单调递增, ;
;………5分
所以
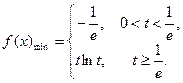 ………6分
………6分(2)
 ,则
,则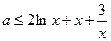 ,对一切
,对一切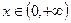 恒成立.……7分
恒成立.……7分设
 ,则
,则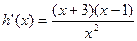 ,
,当
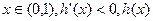 单调递减,
单调递减,当
 单调递增. …………10分
单调递增. …………10分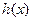 在
在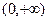 上,有唯一极小值
上,有唯一极小值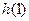 ,即为最小值.
,即为最小值.所以
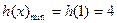 ,因为对一切
,因为对一切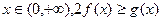 恒成成立,
恒成成立,所以
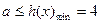 . ……………………………13分
. ……………………………13分略

练习册系列答案
相关题目
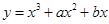 在
在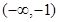 上单调递增,在
上单调递增,在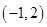 上单调递减,在
上单调递减,在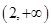 上递增,则
上递增,则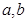 的值为( )
的值为( )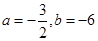
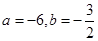
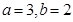
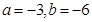 [
[ ,且函数
,且函数 在
在 处有极值,则
处有极值,则 的最大值等于
的最大值等于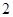
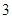


 有绝对值相等,符号相反的极大值和极小值,则常数
有绝对值相等,符号相反的极大值和极小值,则常数 的值是( )
的值是( ) 或
或




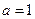 时,求函数
时,求函数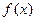 的单调增区间,求函数
的单调增区间,求函数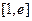 上的最小值;
上的最小值;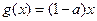 ,若存在
,若存在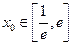 ,使得
,使得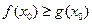 成立,求实数
成立,求实数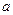 的取值范围。
的取值范围。 在
在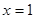 时有极值
时有极值 ,那么
,那么 的值分别为________.
的值分别为________. 的最大值为M,最小值为m,则M+m的值为( )
的最大值为M,最小值为m,则M+m的值为( )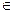 [-3,2]都有f(x)>
[-3,2]都有f(x)>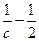 恒成立,求c的取值范围。
恒成立,求c的取值范围。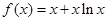 ,若
,若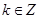 ,且
,且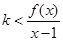 对任意
对任意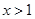 恒成立,则
恒成立,则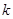 的最大值为_________.
的最大值为_________.