题目内容
已知函数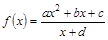 (其中
(其中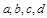 是实数常数,
是实数常数, )
)
(1)若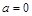 ,函数
,函数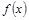 的图像关于点(—1,3)成中心对称,求
的图像关于点(—1,3)成中心对称,求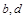 的值;
的值;
(2)若函数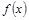 满足条件(1),且对任意
满足条件(1),且对任意 ,总有
,总有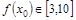 ,求
,求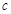 的取值范围;
的取值范围;
(3)若b=0,函数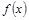 是奇函数,
是奇函数, ,
,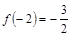 ,且对任意
,且对任意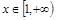 时,不等式
时,不等式 恒成立,求负实数
恒成立,求负实数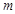 的取值范围.
的取值范围.
(1)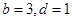 ;(2)
;(2)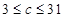 ;(3)
;(3)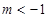 .
.
解析试题分析:(1)由于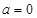 ,
,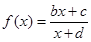 ,这种类型的函数我们易联想到函数
,这种类型的函数我们易联想到函数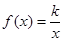 的平移变换,如向右平移
的平移变换,如向右平移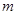 个单位,再向上平移
个单位,再向上平移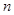 个单位,得函数
个单位,得函数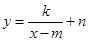 的图象,且函数
的图象,且函数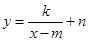 的图象的对称中心就是
的图象的对称中心就是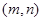 ,因此我们只要把
,因此我们只要把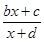 转化为
转化为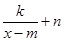 的形式,即
的形式,即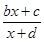
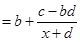 ,就能得出结论;(2)由(1)知,
,就能得出结论;(2)由(1)知, ,问题是当
,问题是当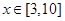 时,函数
时,函数 的值域
的值域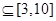 ,可分类讨论,当
,可分类讨论,当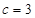 时,
时,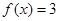
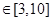 ,而当
,而当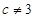 时,函数具有单调性,由此可很快求出函数的最值,求出
时,函数具有单调性,由此可很快求出函数的最值,求出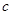 的取值范围;(3)由于
的取值范围;(3)由于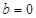 ,
, 中还有三个参数,正好题中有三个条件,我们可先求出
中还有三个参数,正好题中有三个条件,我们可先求出 ,然后才能把不等式
,然后才能把不等式 化为
化为 ,由于
,由于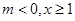 ,因此此分式不等式可以两边同乘以
,因此此分式不等式可以两边同乘以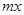 直接去分母化为整式不等式,
直接去分母化为整式不等式,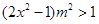 ,从而可以分离参数得
,从而可以分离参数得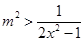 ,也即
,也即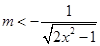 ,下面我们只要求出
,下面我们只要求出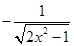 的最小值即可.
的最小值即可.
试题解析:(1)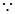
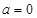 ,
,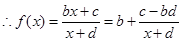 .
.
类比函数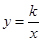 的图像,可知函数
的图像,可知函数 的图像的对称中心是
的图像的对称中心是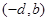 .
.
又函数 的图像的对称中心是
的图像的对称中心是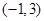 ,
,
(2)由(1)知, .
.
依据题意,对任意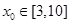 ,恒有
,恒有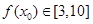 .
.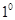 若
若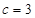 ,则
,则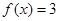 ,符合题意.
,符合题意.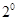 若
若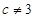 ,当
,当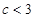 时,对任意
时,对任意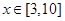 ,恒有
,恒有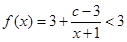 ,不符合题意.
,不符合题意.
所以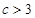 ,函数
,函数 在
在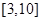 上是单调递减函数,且满足
上是单调递减函数,且满足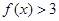 .
.
因此,当且仅当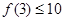 ,即
,即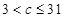 时符合题意.
时符合题意.
综上,所求实数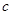 的范围是
的范围是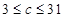 .
.
(3)依据题设,有 解得
解得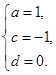
于是,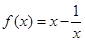 .
.
由 ,解得
,解得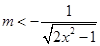 .
.
因此, .
.
考察函数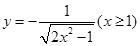 ,可知该函数在
,可知该函数在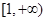 是增函数,故
是增函数,故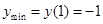 .
.
所以,所求负实数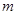 的取值范围是
的取值范围是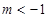 .
.
考点:(1)图象变换;(2)函数的最值;(3)分式不等式与分离参数法求参数取值范围.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案
相关题目
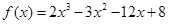 .
. 的单调区间;
的单调区间;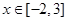 ,求函数
,求函数
 (
( 为常数),函数
为常数),函数 定义为:对每一个给定的实数
定义为:对每一个给定的实数 ,
,
 满足条件
满足条件 时,对于
时,对于 ,
,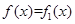 ;
; 是两个实数,满足
是两个实数,满足 ,且
,且 ,若
,若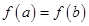 ,求函数
,求函数 上的单调递增区间的长度之和.(闭区间
上的单调递增区间的长度之和.(闭区间 的长度定义为
的长度定义为 )
)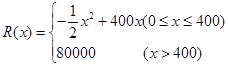 ,其中
,其中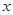 是组合床柜的月产量.
是组合床柜的月产量. 元表示为月产量
元表示为月产量 ,
, .
. ;
;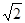 介于
介于 与
与 之间,且距
之间,且距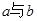 之间的距离是否可能为整数?若有,则求出这个整数;若没有,
之间的距离是否可能为整数?若有,则求出这个整数;若没有,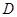 (分贝)由公式
(分贝)由公式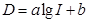 (
(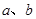 为非零常数)给出,其中
为非零常数)给出,其中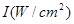 为声音能量.
为声音能量.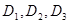 满足
满足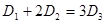 时,求对应的声音能量
时,求对应的声音能量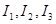 满足的等量关系式;
满足的等量关系式; 时,声音强度为30分贝;当人们正常说话,声音能量为
时,声音强度为30分贝;当人们正常说话,声音能量为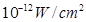 时,声音强度为40分贝.当声音能量大于60分贝时属于噪音,一般人在100分贝~120分贝的空间内,一分钟就会暂时性失聪.问声音能量在什么范围时,人会暂时性失聪.
时,声音强度为40分贝.当声音能量大于60分贝时属于噪音,一般人在100分贝~120分贝的空间内,一分钟就会暂时性失聪.问声音能量在什么范围时,人会暂时性失聪.
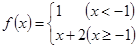 ,
,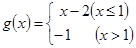 ,
,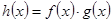
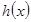 的解析式,并求它的单调递增区间;
的解析式,并求它的单调递增区间;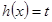 有四个不相等的实数根,求
有四个不相等的实数根,求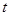 的取值范围。
的取值范围。