题目内容
若曲线y=x3在点P(1,1)处的切线与直线ax-by-2=0互相垂直,则
=
| a |
| b |
-
| 1 |
| 3 |
-
.| 1 |
| 3 |
分析:求导函数,求得切线的斜率,利用曲线y=x3在点P(1,1)处的切线与直线ax-by-2=0互相垂直,即可求得结论.
解答:解:求导函数,可得y′=3x2,当x=1时,y′=3,
∵y=x3在点P(1,1)处的切线与直线ax-by-2=0互相垂直,
∴3•
=-1
∴
=-
故答案为:-
∵y=x3在点P(1,1)处的切线与直线ax-by-2=0互相垂直,
∴3•
| a |
| b |
∴
| a |
| b |
| 1 |
| 3 |
故答案为:-
| 1 |
| 3 |
点评:本题考查导数的几何意义,考查直线的位置关系,考查学生的计算能力,属于基础题.

练习册系列答案
相关题目
 =________.
=________.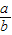 = .
= .