题目内容
若曲线y=x3在点P处的切线的斜率等于3,则点P的坐标为( )
分析:求导函数,利用曲线y=x3在点P处的切线的斜率等于3,建立方程,求出P的横坐标,即可得出点P的坐标.
解答:解:设切点坐标为(t,t3),则
∵f′(x)=3x2,若曲线y=x3在点P处的切线的斜率等于3,
∴f′(t)=3t2=3,
∴t=1或t=-1.
∴点P的坐标为(-1,-1)或(1,1).
故选C.
∵f′(x)=3x2,若曲线y=x3在点P处的切线的斜率等于3,
∴f′(t)=3t2=3,
∴t=1或t=-1.
∴点P的坐标为(-1,-1)或(1,1).
故选C.
点评:本题考查导数知识的运用,考查导数的几何意义,考查学生的计算能力,属于基础题.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
 =________.
=________.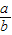 = .
= .