题目内容
已知函数f(x)=(1)若曲线f(x)在点(1,f(1))处的切线与直线2x-y+1=0平行,求a的值;
(2)设g(x)=f′(x)-ax-4,若对一切|a|≤1,都有g(x)<0恒成立,求x的取值范围;
(3)设a=-p2时,若函数f(x)的图象与直线y=2只有一个公共点,求实数p的取值范围.
解:(1)f′(x)=4x2+a,f′(1)=4+a=2,
所以a=-2.
(2)g(x)=f′(x)-ax-4=4x2-ax+a-4,
令φ(a)=(1-x)a+4x2-4,因为对一切|a|≤1,都有g(x)<0恒成立等价于对一切|a|≤1,都有φ(a)<0恒成立,所以![]() 即
即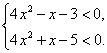 解得
解得![]() <x<1.
<x<1.
则当x∈(![]() ,1)时,对一切|a|≤1,都有g(x)<0恒成立.
,1)时,对一切|a|≤1,都有g(x)<0恒成立.
(3)当a=-p2时,f′(x)=4x2-p2.
①当p=0时,f(x)=![]() x3-1在(-∞,+∞)上单调递增,
x3-1在(-∞,+∞)上单调递增,
所以函数f(x)的图象与直线y=2有一个公共点.
②当p≠0时,f′(x)=(2x+|p|)(2x-|p|).
令f′(x)=0,得x=±![]() .
.
所以当x∈(-∞,![]() ),x∈(
),x∈(![]() ,+∞)时,f′(x)>0,f(x)单调递增,
,+∞)时,f′(x)>0,f(x)单调递增,
当x∈(-![]() ,
,![]() )时,f′(x)<0,f(x)单调递减.
)时,f′(x)<0,f(x)单调递减.
因此f(x)的极小值f(![]() )=
)=![]() (
(![]() )3+(-p)2
)3+(-p)2![]() -1=-
-1=-![]() p2|p|-1<-1.
p2|p|-1<-1.
又f(x)的值域为R,当x∈(![]() ,+∞)时,f(x)单调递增,则一定与直线y=2有交点,
,+∞)时,f(x)单调递增,则一定与直线y=2有交点,
因此只要f(![]() <2即可.
<2即可.
而f(![]() )=
)=![]() (
(![]() )3-p2(
)3-p2(![]() )-1=
)-1=![]() |p|3-1<2.
|p|3-1<2.
解得![]() <p<
<p<![]() ,且p≠0.
,且p≠0.
综上①②可得实数p的取值范围是![]() <p<
<p<![]() .
.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目