题目内容
已知圆心在第一象限的圆C的半径为2
,且与直线x+2y-6=0切于点P(2,2).
(1)求圆C的方程;
(2)从圆C外一点P引圆C的切线PT,T为切点,且PT=PO(O为坐标原点),求PT的最小值.
| 5 |
(1)求圆C的方程;
(2)从圆C外一点P引圆C的切线PT,T为切点,且PT=PO(O为坐标原点),求PT的最小值.
分析:(1)求出过点P(2,2)且与直线x+2y-6=0垂直的直线方程,因为圆心在该直线上,设出圆心坐标,由圆心到切线的距离等于半径求出圆心坐标,则圆的方程可求;
(2)设出P点的坐标,由PT=PO列式得到P点的轨迹为直线,然后求出O到该直线的距离即为PT的最小值.
(2)设出P点的坐标,由PT=PO列式得到P点的轨迹为直线,然后求出O到该直线的距离即为PT的最小值.
解答:解:(1)过点P(2,2)且与直线x+2y-6=0垂直的直线方程为2x-y-2=0,
故可设圆的圆心为(a,2a-2),则
=2
,解得a=4或a=0,
因为圆心在第一象限,故圆心坐标为(4,6),
所以圆的方程为(x-4)2+(y-6)2=20;
(2)设P(x,y),则PO=
,PT=
,
由PT=PO得,2x+3y-8=0,
所以PTmin=POmin=
=
.
即PT的最小值为
.
故可设圆的圆心为(a,2a-2),则
| |a+4a-4-6| | ||
|
| 5 |
因为圆心在第一象限,故圆心坐标为(4,6),
所以圆的方程为(x-4)2+(y-6)2=20;
(2)设P(x,y),则PO=
| x2+y2 |
| (x-4)2+(y-6)2-20 |
由PT=PO得,2x+3y-8=0,
所以PTmin=POmin=
| 8 | ||
|
8
| ||
| 13 |
即PT的最小值为
8
| ||
| 13 |
点评:本题考查了直线与圆的关系,考查了数学转化思想方法,训练了点到直线的距离公式,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
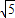 ,且与直线x+2y-6=0切于点P(2,2).
,且与直线x+2y-6=0切于点P(2,2).