题目内容
已知x,y为锐角,且满足cos x= ,cos(x+y)=
,cos(x+y)= ,则sin y的值是( )
,则sin y的值是( )A.

B.

C.

D.

【答案】分析:依题意求出sinx的值,通过cos(x+y)= ,求出sin(x+y)的值,然后利用y=x+y-x的关系求解sin y的值.
,求出sin(x+y)的值,然后利用y=x+y-x的关系求解sin y的值.
解答:解:已知x,y为锐角,且满足cos x= ,sinx=
,sinx= ;cos(x+y)=
;cos(x+y)= ,sin(x+y)=
,sin(x+y)=
sin y=sim(x+y-x)=sin(x+y)cosx-cos(x+y)sinx=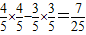
故选C
点评:本题考查两角和与差的正弦函数,考查计算能力,其中角的变换技巧y=x+y-x是解题关键,注意三角函数象限符号,本题是基础题.
 ,求出sin(x+y)的值,然后利用y=x+y-x的关系求解sin y的值.
,求出sin(x+y)的值,然后利用y=x+y-x的关系求解sin y的值.解答:解:已知x,y为锐角,且满足cos x=
 ,sinx=
,sinx= ;cos(x+y)=
;cos(x+y)= ,sin(x+y)=
,sin(x+y)=
sin y=sim(x+y-x)=sin(x+y)cosx-cos(x+y)sinx=
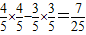
故选C
点评:本题考查两角和与差的正弦函数,考查计算能力,其中角的变换技巧y=x+y-x是解题关键,注意三角函数象限符号,本题是基础题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
已知x,y为锐角,且满足cos x=
,cos(x+y)=
,则sin y的值是( )
| 4 |
| 5 |
| 3 |
| 5 |
A、
| ||
B、
| ||
C、
| ||
D、
|
 ,cos(x+y)=
,cos(x+y)= ,则sin y的值是( )
,则sin y的值是( )



 ,cos(x+y)=
,cos(x+y)= ,则sin y的值是( )
,则sin y的值是( )


