题目内容
某车间共有12名工人,随机抽取6名,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数.

(1)若日加工零件个数大于样本均值的工人为优秀工人,根据茎叶图推断该车间12名工人中有几名优秀工人?
(2)从这6名工人中任取2人,设这两人加工零件的个数分别为 ,求
,求 的概率.
的概率.

(1)若日加工零件个数大于样本均值的工人为优秀工人,根据茎叶图推断该车间12名工人中有几名优秀工人?
(2)从这6名工人中任取2人,设这两人加工零件的个数分别为
 ,求
,求 的概率.
的概率.(1)4;(2)

试题分析:(1)根据平均数公式先求样本平均数,从样本中找出比平均数大的数共有几个,根据频数除以总数得到样本中优秀工人的频率,将总数12乘以此频率可得优秀工人总数。(2)从6人中任取2人其加工零件数所包含的基本事件一一例举出,得到基本事件总数。再将其中符合
 的事件一一例举并得到包含的基本事件数,根据古典概型概率公式即可求得所求概率。
的事件一一例举并得到包含的基本事件数,根据古典概型概率公式即可求得所求概率。(1)样本均值为
 , 2分
, 2分样本中大于22的有2人,样本的优秀率为
 , 4分
, 4分∴12名工人中优秀工人为:12
 人. 5分
人. 5分(2)6人中任取2人,加工的零件个数构成基本事件:(17,19),(17,20),(17,21),(17,25),(17,30),(19,20),(19,21),(19,25),(19,30),(20,21),(20,25),(20,30),(21,25),(21,30),(25,30)共15个基本事件. 7分
其中满足“
 ”的事件有:(17,19), (19,20), (19,21), (20,21)共4个. 9分
”的事件有:(17,19), (19,20), (19,21), (20,21)共4个. 9分故所求概率为
 . 10分
. 10分
练习册系列答案
相关题目

 本月价格指数
本月价格指数 上月价格指数. 规定:当
上月价格指数. 规定:当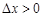 时,称本月价格指数环比增长;
时,称本月价格指数环比增长; 时,称本月价格指数环比下降;当
时,称本月价格指数环比下降;当 时,称本月价格指数环比持平.
时,称本月价格指数环比持平. 

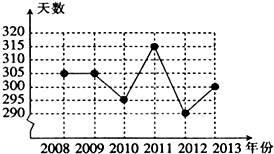
 ,且平均气温低于22.5℃的采集点个数为11,则平均气温不低于25.5℃的采集点个数为( )
,且平均气温低于22.5℃的采集点个数为11,则平均气温不低于25.5℃的采集点个数为( )
