题目内容
图中多面体是过正四棱柱的底面正方形ABCD的顶点A作截面AB1C1D1而截得的,且B1B=D1D。已知截面AB1C1D1与底面ABCD成30度的二面角,AB=1,则这个多面体的体积为( )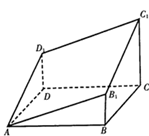
A.
B.
C.
D.
D
解析试题分析:作D1E∥DC,连接B1D1,B1E,BD,则几何体被分割成两个棱锥与一个棱柱
∵截面AB1C1D1与底面成30°的二面角,∴∠CAC1=30°
∵AB=1,∴DD1= ,∴CC1=
,∴CC1= ∴VA-BDD1B1=
∴VA-BDD1B1=
VBDC-B1D1C1= ∴多面体的体积为
∴多面体的体积为 ,故选D.
,故选D.
考点:本题主要是考查几何体的体积,关键是将几何体进行分割,利用规则几何体的体积公式求解.
点评:解决该试题的关键是作D1E∥DC,连接B1D1,B1E,BD,则几何体被分割成两个棱锥与一个棱柱,分别求出两个棱锥与一个棱柱的体积,即可得多面体的体积

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
过空间任意一点引三条不共面的直线,它们所确定的平面个数是( )
| A.1 | B.2 | C.3 | D.1或3 |
若一个球的表面积为4 ,则这个球的体积是( )
,则这个球的体积是( )
A. | B. | C. | D. |
某四棱锥的三视图如图所示,该四棱锥的表面积是 ( )
| A.32 | B.16+ | C.48 | D. |
 ,由它的互不相邻的四个顶点连线所构成的四面体的体积是( )
,由它的互不相邻的四个顶点连线所构成的四面体的体积是( )



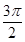



 的正方形
的正方形 沿对角线
沿对角线 折起,使得平面
折起,使得平面 平面
平面 ,在折起后形成的三棱锥
,在折起后形成的三棱锥 中,给出下列三个命题:
中,给出下列三个命题: 是等边三角形; ②
是等边三角形; ② ; ③三棱锥
; ③三棱锥 .
.





