题目内容
【题目】设函数f(x)=x2+aln(x+1)(a为常数)
(Ⅰ)若函数y=f(x)在区间[1,+∞)上是单调递增函数,求实数a的取值范围;
(Ⅱ)若函数y=f(x)有两个极值点x1 , x2 , 且x1<x2 , 求证: ![]() .
.
【答案】解:(Ⅰ)根据题意知:f′(x)= ![]() 在[1,+∞)上恒成立. 即a≥﹣2x2﹣2x在区间[1,+∞)上恒成立.
在[1,+∞)上恒成立. 即a≥﹣2x2﹣2x在区间[1,+∞)上恒成立.
∵﹣2x2﹣2x在区间[1,+∞)上的最大值为﹣4,
∴a≥﹣4;
经检验:当a=﹣4时, 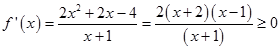 ,x∈[1,+∞).
,x∈[1,+∞).
∴a的取值范围是[﹣4,+∞).
(Ⅱ) ![]() 在区间(﹣1,+∞)上有两个不相等的实数根,
在区间(﹣1,+∞)上有两个不相等的实数根,
即方程2x2+2x+a=0在区间(﹣1,+∞)上有两个不相等的实数根.
记g(x)=2x2+2x+a,则有 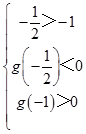 ,解得
,解得 ![]() .
.
∴ ![]() ,
, ![]() .
.
∴ 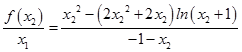
令 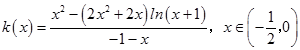 .
.![]() ,
,
记 ![]() .
.
∴ ![]() ,
,![]() .
.
在 ![]() 使得p′(x0)=0.
使得p′(x0)=0.
当 ![]() ,p′(x)<0;当x∈(x0 , 0)时,p′(x)>0.
,p′(x)<0;当x∈(x0 , 0)时,p′(x)>0.
而k′(x)在 ![]() 单调递减,在(x0 , 0)单调递增,
单调递减,在(x0 , 0)单调递增,
∵ ![]() ,
,
∴当 ![]() ,
,
∴k(x)在 ![]() 单调递减,
单调递减,
即 ![]()
【解析】(Ⅰ)已知原函数的值为正,得到导函数的值非负,从而求出参量的范围;(Ⅱ)利用韦达定理,对所求对象进行消元,得到一个新的函数,对该函数求导后,再对导函数求导,通过对导函数的导导函数的研究,得到导函数的最值,从而得到原函数的最值,即得到本题结论.
【考点精析】关于本题考查的利用导数研究函数的单调性和函数的最大(小)值与导数,需要了解一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;求函数
在这个区间单调递减;求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值才能得出正确答案.
比较,其中最大的是一个最大值,最小的是最小值才能得出正确答案.

 应用题作业本系列答案
应用题作业本系列答案【题目】为普及高中生安全逃生知识与安全防护能力,某学校高一年级举办了高中生安全知识与安全逃生能力竞赛.该竞赛分为预赛和决赛两个阶段,预赛为笔试,决赛为技能比赛.先将所有参赛选手参加笔试的成绩(得分均为整数,满分为100分)进行统计,制成如下频率分布表.
分数(分数段) | 频数(人数) | 频率 |
[60,70) | 9 | x |
[70,80) | y | 0.38 |
[80,90) | 16 | 0.32 |
[90,100) | z | s |
合计 | p | 1 |
(Ⅰ)求出上表中的x,y,z,s,p的值;
(Ⅱ)按规定,预赛成绩不低于90分的选手参加决赛,参加决赛的选手按照抽签方式决定出场顺序.已知高一二班有甲、乙两名同学取得决赛资格.
①求决赛出场的顺序中,甲不在第一位、乙不在最后一位的概率;
②记高一二班在决赛中进入前三名的人数为X,求X的分布列和数学期望.
