题目内容
已知2x≤256且log2x≥
,求函数f(x)=log2
•log
的最大值和最小值.
| 1 |
| 2 |
| x |
| 2 |
| 2 |
| ||
| 2 |
由2x≤256且log2x≥
,可解得
≤x≤8,
则f(x)的定义域为[
,8],
f(x)=log2
•log
=(log2x-1)×(log2x-2)=(log2x-
) 2-
由f(x)的定义域为[
,8],即3≥log2x≥
故函数的最大值是f(8)=2
最小值是-
答:函数f(x)=log2
•log
的最大值和最小值分别为2与-
.
| 1 |
| 2 |
| 2 |
则f(x)的定义域为[
| 2 |
f(x)=log2
| x |
| 2 |
| 2 |
| ||
| 2 |
| 3 |
| 2 |
| 1 |
| 4 |
由f(x)的定义域为[
| 2 |
| 1 |
| 2 |
故函数的最大值是f(8)=2
最小值是-
| 1 |
| 4 |
答:函数f(x)=log2
| x |
| 2 |
| 2 |
| ||
| 2 |
| 1 |
| 4 |

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
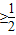 ,
,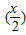 •log
•log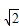
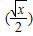 的最大值和最小值.
的最大值和最小值.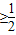 ,
, •log
•log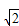
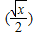 的最大值和最小值.
的最大值和最小值.