题目内容
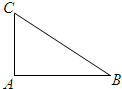 如图,在Rt△ABC中,∠CAB=90°,|AB|=2,|AC|=
如图,在Rt△ABC中,∠CAB=90°,|AB|=2,|AC|=| 3 | 2 |
(1)建立适当的坐标系,求曲线E的方程;
(2)设点Q是曲线E上的一动点,求线段QA中点的轨迹方程;
(3)设M,N是曲线E上不同的两点,直线CM和CN的倾斜角互补,试判断直线MN的斜率是否为定值.如果是,求这个定值;如果不是,请说明理由.
(4)若点D是曲线E上的任一定点(除曲线E与直线AB的交点),M,N是曲线E上不同的两点,直线DM和DN的倾斜角互补,直线MN的斜率是否为定值呢?如果是,请你指出这个定值.(本小题不必写出解答过程)
分析:(1)由于曲线E上任一点到A,B两点的距离之和不变,所以其轨迹是椭圆,求方程先建立坐标系,从而可求;
(2)先假设线段QA中点的坐标P,利用中点坐标公式得出P,Q坐标之间的关系,再结合(1)求出线段QA中点的轨迹方程;
(3)由于直线CM和CN的倾斜角互补,所以可设直线CM和CN的斜率分别为k,-k,再结合M,N是曲线E上不同的两点,可知直线MN的斜率是定值;
(4)利用极限位置考虑:当直线DM和DN的倾斜角都为90°时,直线MN即为D'(a,-b)处的切线.
(2)先假设线段QA中点的坐标P,利用中点坐标公式得出P,Q坐标之间的关系,再结合(1)求出线段QA中点的轨迹方程;
(3)由于直线CM和CN的倾斜角互补,所以可设直线CM和CN的斜率分别为k,-k,再结合M,N是曲线E上不同的两点,可知直线MN的斜率是定值;
(4)利用极限位置考虑:当直线DM和DN的倾斜角都为90°时,直线MN即为D'(a,-b)处的切线.
解答: 解:(1)以AB的中点为原点,AB所在直线为x轴建立直角坐标系.
解:(1)以AB的中点为原点,AB所在直线为x轴建立直角坐标系.
∵|CA|+|CB|=4[(1分)]
不难知道:曲线E是以A,B为两焦点、长轴长为4的椭圆.
故曲线E的方程为
+
=1,
(2)设线段QA的中点为P(x,y),∵A(-1,0),
∴Q(2x+1,2y)[(5分)]
∵点Q在曲线E上,故可得:
+
=1[(7分)]
即线段QA中点的轨迹方程为(x+
)2+
=1[(8分)]
(3)设直线CM和CN的斜率分别为k,-k
直线CM的直线方程为y-
=k(x+1)
代入曲线E的方程,得(3+4k2)x2+8k(k+
)x+4k2+12k-3=0[(9分)]
由韦达定理:xC•xM=
,
∴xM=-
同理xN=-
[(10分)]
而yM-
=k(xM+1),yN-
=-k(xN+1)
∴kMN=
=
=
=
故直线MN的斜率为定值
[(12分)]
(4)设D(a,b),当直线DM和DN的倾斜角都为90°时,直线MN即为D'(a,-b)处的切线,则直线MN的斜率为定值
 解:(1)以AB的中点为原点,AB所在直线为x轴建立直角坐标系.
解:(1)以AB的中点为原点,AB所在直线为x轴建立直角坐标系.∵|CA|+|CB|=4[(1分)]
不难知道:曲线E是以A,B为两焦点、长轴长为4的椭圆.
故曲线E的方程为
| x2 |
| 4 |
| y2 |
| 3 |
(2)设线段QA的中点为P(x,y),∵A(-1,0),
∴Q(2x+1,2y)[(5分)]
∵点Q在曲线E上,故可得:
| (2x+1)2 |
| 4 |
| (2y)2 |
| 3 |
即线段QA中点的轨迹方程为(x+
| 1 |
| 2 |
| 4y2 |
| 3 |
(3)设直线CM和CN的斜率分别为k,-k
直线CM的直线方程为y-
| 3 |
| 2 |
代入曲线E的方程,得(3+4k2)x2+8k(k+
| 3 |
| 2 |
由韦达定理:xC•xM=
| 4k2+12k-3 |
| 3+4k2 |

∴xM=-
| 4k2+12k-3 |
| 3+4k2 |
同理xN=-
| 4k2-12k-3 |
| 3+4k2 |
而yM-
| 3 |
| 2 |
| 3 |
| 2 |
∴kMN=
| yM-yN |
| xM-xN |
| k(xM+xN+2) |
| xM-xN |
| ||
|
| 1 |
| 2 |
故直线MN的斜率为定值
| 1 |
| 2 |
(4)设D(a,b),当直线DM和DN的倾斜角都为90°时,直线MN即为D'(a,-b)处的切线,则直线MN的斜率为定值
| 3a |
| 4b |
点评:本题主要考查曲线轨迹方程的求解,涉及定义法、代入法等,同时解决了定值问题.

练习册系列答案
 目标测试系列答案
目标测试系列答案
相关题目
 如图,在Rt△ABC中,∠C=90°,D为BC上一点,∠DAC=30°,BD=2,AB=2
如图,在Rt△ABC中,∠C=90°,D为BC上一点,∠DAC=30°,BD=2,AB=2| 3 |
A、2
| ||||
| B、3 | ||||
C、
| ||||
D、
|
 如图,在Rt△ABC中,AC=1,BC=x,D是斜边AB的中点,将△BCD沿直线CD翻折,若在翻折过程中存在某个位置,使得CB⊥AD,则x的取值范围是( )
如图,在Rt△ABC中,AC=1,BC=x,D是斜边AB的中点,将△BCD沿直线CD翻折,若在翻折过程中存在某个位置,使得CB⊥AD,则x的取值范围是( )A、(0,
| ||||
B、(
| ||||
C、(
| ||||
| D、(2,4] |
 如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于点E.
如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于点E. 如图,在Rt△ABC中,∠ABC=90°,BA=BC=2,AE⊥平面ABC,CD⊥平面ABC,CE交AD于点P.
如图,在Rt△ABC中,∠ABC=90°,BA=BC=2,AE⊥平面ABC,CD⊥平面ABC,CE交AD于点P. 8.如图,在Rt△ABC中,∠CAB=90°,AB=2,AC=
8.如图,在Rt△ABC中,∠CAB=90°,AB=2,AC=