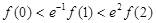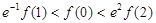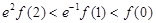题目内容
已知 ,其中
,其中 ,如果存在实数
,如果存在实数 ,使
,使 ,则
,则 的值( )
的值( )
| A.必为正数 | B.必为负数 | C.必为非负数 | D.必为非正数 |
B
解析试题分析:因为, ,
,
所以, f'(x)=x²-2x+a=(x-1)²+(a-1)
所以f'(x)的图象是对称轴为x=1,顶点为(1,a-1),开口向上的抛物线,且f'(t)<0,
所以a<1,
而对称轴与x轴的交点分别为:(1-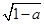 ,0)和 (1+
,0)和 (1+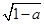 ,0),两交点的水平距离为2。通过观察f'(x)图像可知:因为f'(t)<0,所以t∈(1-
,0),两交点的水平距离为2。通过观察f'(x)图像可知:因为f'(t)<0,所以t∈(1-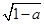 ,1+
,1+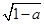 ),
),
①t+2>1+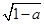 ,所以f'(t+2)>0
,所以f'(t+2)>0
②t∈(1-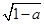 ,1+
,1+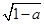 ), 2t+1∈(3-2√
), 2t+1∈(3-2√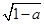 ,3+2
,3+2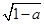 )
)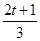 ∈(1-2×
∈(1-2×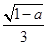 ,1+2×
,1+2×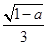 )
)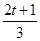 >1-
>1-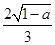 且
且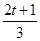 <1+2
<1+2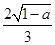
所以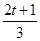 在(1-
在(1-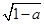 ,1+
,1+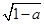 )之间,所以f'(
)之间,所以f'(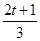 )<0
)<0 为一正数乘以一负数,值必为负数,故选B。
为一正数乘以一负数,值必为负数,故选B。
考点:本题主要考查导数的计算,利用导数研究函数的图象和性质。
点评:中档题,集合导函数是二次函数,因此,应用二次函数的图象和性质,确定导函数值的正负,从确定 的正负。
的正负。

练习册系列答案
相关题目
函数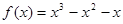 的单调减区间是( )
的单调减区间是( )
A.(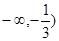 | B.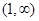 | C.(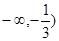 , ,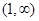 | D.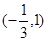 |
由抛物线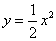 与直线
与直线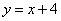 所围成的图形的面积是
所围成的图形的面积是
A.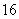 | B.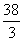 | C.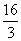 | D.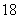 |
已知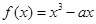 在
在 上递增,则
上递增,则 的范围是( )
的范围是( )
A.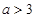 | B. | C.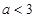 | D.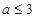 |
已知 ,且
,且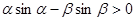 ,则下列不等式一定成立的是( )
,则下列不等式一定成立的是( )
A.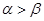 | B.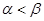 |
C.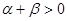 | D.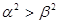 |
函数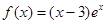 的单调递增区间是( )
的单调递增区间是( )
A.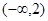 | B.(0,3) | C.(1,4) | D.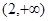 |
一个物体的运动方程为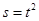 其中
其中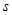 的单位是米,
的单位是米,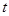 的单位是秒,那么物体,在
的单位是秒,那么物体,在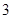 秒末的瞬时速度是 米/秒
秒末的瞬时速度是 米/秒
A.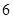 | B. | C.4 | D.2 |
如图,由函数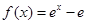 的图象,直线
的图象,直线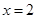 及x轴所围成的阴影部分面积等于( )
及x轴所围成的阴影部分面积等于( )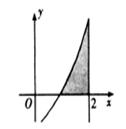
A.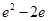 | B.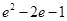 |
C.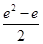 | D.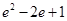 |
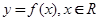 ,的导函数为
,的导函数为 ,且
,且 ,
, ,则下列不等式成立的是(注:e为自然对数的底数)( )
,则下列不等式成立的是(注:e为自然对数的底数)( )