题目内容
 (2012•长春模拟)如图,在底面为直角梯形的四棱锥P-ABCD中AD∥BC,∠ABC=90°,PD⊥平面ABCD,AD=1,AB=
(2012•长春模拟)如图,在底面为直角梯形的四棱锥P-ABCD中AD∥BC,∠ABC=90°,PD⊥平面ABCD,AD=1,AB=| 3 |
(1)求证:BD⊥PC;
(2)当PD=1时,求此四棱锥的表面积.
分析:(1)通过证明BD⊥DC,BD⊥PD,证明BD⊥平面PDC,然后推出BD⊥PC;
(2)利用PD⊥平面ABCD,证明AB⊥平面PAD,分别求出SRt△PAB,S△PBC,SRt△PDA,SRt△PDC,S梯形ABCD,然后求出四棱锥的表面积.
(2)利用PD⊥平面ABCD,证明AB⊥平面PAD,分别求出SRt△PAB,S△PBC,SRt△PDA,SRt△PDC,S梯形ABCD,然后求出四棱锥的表面积.
解答: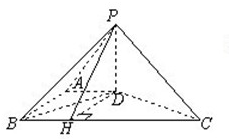 解:(1)证明:由题意可知DC=2
解:(1)证明:由题意可知DC=2
,则,
BC2=DB2+DC2,∴BD⊥DC,
∵PD⊥平面ABCD,
∴BD⊥PD,而PD∩CD=D,
∴BD⊥平面PDC.∵PC?平面PDC,
∴BD⊥PC;
(2)∵PD⊥平面ABCD,∴PD⊥AB,而AB⊥AD,PD∩AD=D,
∴AB⊥平面PAD,∴AB⊥PA,即是直角三角形.
SRt△PAB=
AB• PB=
•
•
=
.
过D作DH⊥BC于点H,连接PH,
则同理可证PH⊥BC.并且PH=
=2,
S△PBC=
BC•PH=
×4×2=4.
易得SRt△PDA=
AD• PD=
•1•1=
,
SRt△PDC=
DC• PD=
•2
•1=
,
S梯形ABCD=
(AD+ BC)•AB=
(1+4)•
=
.
故此四棱锥的表面积为:
SRt△PAB+S△PBC+SRt△PDA+SRt△PDC+S梯形ABCD
=
+4+
+
+
=
.
 解:(1)证明:由题意可知DC=2
解:(1)证明:由题意可知DC=2| 3 |
BC2=DB2+DC2,∴BD⊥DC,
∵PD⊥平面ABCD,
∴BD⊥PD,而PD∩CD=D,
∴BD⊥平面PDC.∵PC?平面PDC,
∴BD⊥PC;
(2)∵PD⊥平面ABCD,∴PD⊥AB,而AB⊥AD,PD∩AD=D,
∴AB⊥平面PAD,∴AB⊥PA,即是直角三角形.
SRt△PAB=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| ||
| 2 |
过D作DH⊥BC于点H,连接PH,
则同理可证PH⊥BC.并且PH=
1+(
|
S△PBC=
| 1 |
| 2 |
| 1 |
| 2 |
易得SRt△PDA=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
SRt△PDC=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
S梯形ABCD=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
5
| ||
| 2 |
故此四棱锥的表面积为:
SRt△PAB+S△PBC+SRt△PDA+SRt△PDC+S梯形ABCD
=
| ||
| 2 |
| 1 |
| 2 |
| 3 |
5
| ||
| 2 |
9+7
| ||||
| 2 |
点评:本题考查直线与直线的垂直,直线与平面垂直,几何体的表面积的求法,考查空间想象能力计算能力.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案
相关题目
 (2012•长春模拟)一个空间几何体的正视图和侧视图都是边长为1的正方形,俯视图是一个直径为1的圆,那么这个几何体的体积为( )
(2012•长春模拟)一个空间几何体的正视图和侧视图都是边长为1的正方形,俯视图是一个直径为1的圆,那么这个几何体的体积为( )