题目内容
盒内有大小相同的9个球,其中2个红色球,3个白色球,4个黑色球. 规定取出1个红色球得1分,取出1个白色球得0分,取出1个黑色球得-1分 . 现从盒内任取3个球
(Ⅰ)求取出的3个球中至少有一个红球的概率;
(Ⅱ)求取出的3个球得分之和恰为1分的概率;
(Ⅲ)设 为取出的3个球中白色球的个数,求
为取出的3个球中白色球的个数,求 的分布列.
的分布列.
【答案】
(Ⅰ)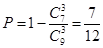 ;(Ⅱ)
;(Ⅱ)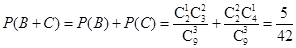 .
.
(Ⅲ)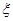 的分布列为:
的分布列为:
|
|
0 |
1 |
2 |
3 |
|
|
|
|
|
|
【解析】
试题分析:(Ⅰ)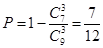 3分
3分
(Ⅱ)记 “取出1个红色球,2个白色球”为事件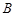 ,“取出2个红色球, 1个黑色球”为事件
,“取出2个红色球, 1个黑色球”为事件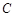 ,则
,则 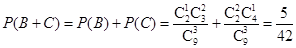 . 6分
. 6分
(Ⅲ)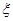 可能的取值为
可能的取值为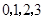 . 7分
. 7分
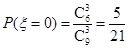 ,
, 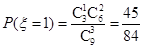 ,
,
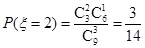 ,
, 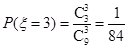 . 11分
. 11分
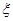 的分布列为:
的分布列为:
|
|
0 |
1 |
2 |
3 |
|
|
|
|
|
|
考点:互斥事件的概率,随机变量的分布列。
点评:中档题,计算事件的概率,关键是明确所研究的事件,当涉及互斥事件、对立事件、独立事件等事件的概率计算问题时,灵活运用有关公式。随机变量的分布列,关键是概率的计算。注意应用各概率之和为1,加以验证。

练习册系列答案
相关题目
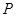
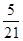
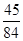
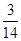
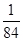
 为取出的3个球中白色球的个数,求
为取出的3个球中白色球的个数,求