题目内容
17.已知一个棱锥的三视图如图,根据图中标出的尺寸(单位:cm),可得这个棱锥的侧面积是4+4$\sqrt{2}$+2$\sqrt{3}$(cm2)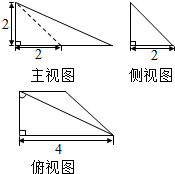
分析 根据几何体的三视图,得出该几何体是一个以俯视图为底面的四棱锥,计算出各个侧面的面积,相加即可.
解答  解:由已知的三视图可得:该几何体直观图如下:
解:由已知的三视图可得:该几何体直观图如下:
其中PA⊥底面ABCD,
PA=AB=AD=2cm,BC=4cm,底面ABCD是以AB为直角角的直角梯形,
所以S△PAB=S△PAD=$\frac{1}{2}$×2×2=2cm2,
PB=PD=CD=2$\sqrt{2}$cm,AC=2$\sqrt{5}$cm,PC=2$\sqrt{6}$cm,
所以PB⊥BC,S△PBC=$\frac{1}{2}$×2$\sqrt{2}$×4=4$\sqrt{2}$cm2,
等腰△PCD底边PC上的高为:$\sqrt{{(2\sqrt{2})}^{2}{-(\frac{2\sqrt{6}}{2})}^{2}}$=$\sqrt{2}$cm,
所以S△PCD=$\frac{1}{2}$×2$\sqrt{6}$×$\sqrt{2}$=2$\sqrt{3}$cm2,
所以棱锥的侧面积S=2×2+4$\sqrt{2}$+2$\sqrt{3}$=4+4$\sqrt{2}$+2$\sqrt{3}$cm2,.
故答案为:4+4$\sqrt{2}$+2$\sqrt{3}$cm2
点评 本题考查了根据几何体的三视图求表面积的应用问题,解题的关键是根据三视图得出几何体的形状,是基础题目.

练习册系列答案
相关题目
7.计算$\frac{\sqrt{x}•\root{3}{{x}^{4}}}{x•\root{6}{x}}$的值为( )
| A. | ${x}^{\frac{2}{3}}$ | B. | ${x}^{-\frac{2}{3}}$ | C. | ${x}^{\frac{1}{3}}$ | D. | ${x}^{-\frac{1}{3}}$ |
5.已知函数f(x)=$\left\{{\begin{array}{l}{(1-3a)x+10a,x≤7}\\{{a^{x-7}},x>7}\end{array}}$是定义域(-∞,+∞)上的单调递减函数,则实数a的取值范围是( )
| A. | $(\frac{1}{3},\frac{1}{2})$ | B. | ($\frac{1}{3}$,$\frac{6}{11}$] | C. | $[\frac{1}{2},\frac{2}{3})$ | D. | $(\frac{1}{2},\frac{6}{11}]$ |
9.下列四组函数中,表示同一函数的是( )
| A. | $f(x)=|x|,g(x)=\sqrt{x^2}$ | B. | f(x)=lgx2,g(x)=2lgx | ||
| C. | $f(x)=\frac{{{x^2}-1}}{x-1},g(x)=x-1$ | D. | $f(x)=\sqrt{x+1}•\sqrt{x-1},g(x)=\sqrt{{x^2}-1}$ |