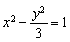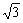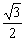题目内容
圆C的圆心在y轴正半轴上,且与x轴相切,被双曲线x2-
=1的渐近线截得的弦长为
,则圆C的方程为( )
| y2 |
| 3 |
| 3 |
分析:设出圆C的方程,求出双曲线x2-
=1的渐近线方程,利用圆被双曲线x2-
=1的渐近线截得的弦长为
,建立方程,即可求出圆C的方程.
| y2 |
| 3 |
| y2 |
| 3 |
| 3 |
解答:解:设圆C的方程为x2+(y-a)2=a2(a>0),圆心坐标为(0,a),
∵双曲线x2-
=1的渐近线方程为y=±
x,圆被双曲线x2-
=1的渐近线截得的弦长为
,
∴(
)2+(
)2=a2,
∴a=1,
∴圆C的方程为x2+(y-1)2=1.
故选A.
∵双曲线x2-
| y2 |
| 3 |
| 3 |
| y2 |
| 3 |
| 3 |
∴(
| ||
| 2 |
| a |
| 2 |
∴a=1,
∴圆C的方程为x2+(y-1)2=1.
故选A.
点评:本题考查双曲线的几何性质,考查直线与圆的位置关系,正确运用勾股定理是关键.

练习册系列答案
相关题目
 (2013•揭阳二模)如图已知抛物线C:y2=2px(p>0)的准线为l,焦点为F,圆M的圆心在x轴的正半轴上,且与y轴相切.过原点作倾斜角为
(2013•揭阳二模)如图已知抛物线C:y2=2px(p>0)的准线为l,焦点为F,圆M的圆心在x轴的正半轴上,且与y轴相切.过原点作倾斜角为 (2013•揭阳二模)如图已知抛物线C:y2=2px(p>0)的准线为l,焦点为F,圆M的圆心在x轴的正半轴上,且与y轴相切.过原点作倾斜角为
(2013•揭阳二模)如图已知抛物线C:y2=2px(p>0)的准线为l,焦点为F,圆M的圆心在x轴的正半轴上,且与y轴相切.过原点作倾斜角为