题目内容
已知椭圆,椭圆左焦点为,为坐标原点,是椭圆上一点,点在线段上,且,,则点的横坐标为
(A) (B) (C) (D)
D
解析考点:椭圆的简单性质;平面向量的坐标运算.
专题:计算题;圆锥曲线的定义、性质与方程.
分析:先确定OM为△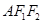 的中位线,利用| OM |=2,可得|AF
的中位线,利用| OM |=2,可得|AF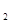 |=4,再利用椭圆的定义可得结论.
|=4,再利用椭圆的定义可得结论.
解答:解:∵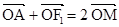
∴M为AF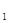 的中点
的中点
∴OM为△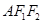 的中位线
的中位线
∵| OM |=2
∴|AF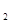 |=4
|=4
设点A的横坐标为x,则由椭圆的定义可得:
∴|AF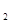 |=a-ex=3-
|=a-ex=3-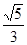 x=4
x=4
∴x=-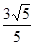
故选D.
点评:本题考查向量知识,考查三角形中位线的性质,考查椭圆的定义,属于中档题.

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
.已知点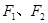 为椭圆
为椭圆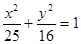 的左右焦点,过
的左右焦点,过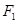 的直线
的直线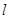 交该椭圆于
交该椭圆于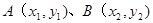 两点,
两点,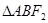 的内切圆的周长为
的内切圆的周长为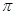 ,则
,则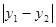 的值是( )
的值是( )
A.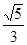 | B.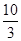 | C.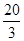 | D.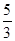 |
已知两点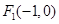 、
、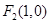 ,且
,且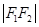 是
是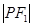 与
与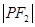 的等差中项,则动点
的等差中项,则动点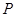 的轨迹方程是( )
的轨迹方程是( )
A.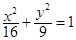 | B.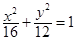 | C.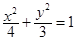 | D.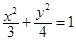 |
正三角形的一个顶点位于原点,另外两个顶点在抛物线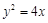 上,则这个正三角形的边长为( )
上,则这个正三角形的边长为( )
A.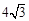 | B.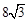 | C.8 | D.16 |
如果椭圆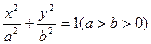 的离心率为
的离心率为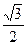 ,那么双曲线
,那么双曲线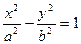 的离心率是 ( )
的离心率是 ( )
A.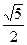 | B. | C.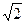 | D.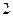 |
已知双曲线的两个焦点为F1(-,0)、F2(,0),M是此双曲线上的一点,且 满足
满足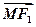 ·
·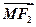 =0,|
=0,|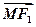 |·|
|·|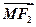 |=2,则该双曲线的方程是( )
|=2,则该双曲线的方程是( )
| A.-y2=1 | B.x2-=1 | C.-=1 | D.-=1 |
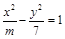 ,直线l过其左焦点F1,交双曲线左支于A、B两点,且|AB|=4,F2为双曲线的右焦点,△ABF2的周长为20,则m的值为 ( )
,直线l过其左焦点F1,交双曲线左支于A、B两点,且|AB|=4,F2为双曲线的右焦点,△ABF2的周长为20,则m的值为 ( ) 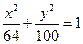 的准线方程是
的准线方程是
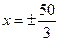

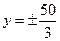

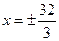

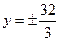
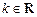 ,则“
,则“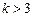 ”是“方程
”是“方程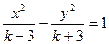 表示双曲线”
表示双曲线” )充要条件 ( D)既不充分也不必要条件
)充要条件 ( D)既不充分也不必要条件