题目内容
已知函数![]() R,且
R,且![]() .
.
(1)当![]() 时,若函数
时,若函数![]() 存在单调递减区间,求
存在单调递减区间,求![]() 的取值范围;
的取值范围;
(2)当![]() 且
且![]() 时,讨论函数
时,讨论函数![]() 的零点个数.
的零点个数.
解析:(1)当![]() 时,函数
时,函数![]()
![]() ,其定义域是
,其定义域是![]() ,
,
∴![]() .
.
![]() 函数
函数![]() 存在单调递减区间,
存在单调递减区间,
∴![]()
![]() 在
在![]() 上有无穷多个解.
上有无穷多个解.
∴关于![]() 的不等式
的不等式![]() 在
在![]() 上有无穷多个解.
上有无穷多个解.
① 当![]() 时,函数
时,函数![]() 的图象为开口向上的抛物线,
的图象为开口向上的抛物线,
关于![]() 的不等式
的不等式![]() 在
在![]() 上总有无穷多个解.
上总有无穷多个解.
② 当![]() 时,函数
时,函数![]() 的图象为开口向下的抛物线,其对称轴为
的图象为开口向下的抛物线,其对称轴为
![]() .要使关于
.要使关于![]() 的不等式
的不等式![]() 在
在![]() 上有无穷多个解.
上有无穷多个解.
必须![]() ,
,
解得![]() ,此时
,此时![]() .
.
综上所述,![]() 的取值范围为
的取值范围为![]() .
.
另解:分离系数:不等式![]() 在
在![]() 上有无穷多个解,
上有无穷多个解,
则关于![]() 的不等式
的不等式![]() 在
在![]() 上有无穷多个解,
上有无穷多个解,
∴![]() ,即
,即![]() ,而
,而![]() .
.
∴![]() 的取值范围为
的取值范围为![]() .
.
(2)当![]() 时,函数
时,函数![]()
![]() ,其定义域是
,其定义域是![]() ,
,
∴![]() .
.
令![]() ,得
,得![]() ,即
,即![]() ,
,
![]() ,
,
![]() ,
,![]() ,则
,则![]() ,
,
∴![]()
当![]()
![]() 时,
时,![]() ;当
;当![]() 1时,
1时,![]() .
.
∴函数![]() 在区间
在区间![]() 上单调递增,在区间
上单调递增,在区间![]() 上单调递减.
上单调递减.
∴当![]() 时,函数
时,函数![]() 取得最大值,其值为
取得最大值,其值为![]() .
.
① 当![]() 时,
时,![]() ,若
,若![]() , 则
, 则![]() , 即
, 即![]() .
.
此时,函数![]() 与
与![]() 轴只有一个交点,故函数
轴只有一个交点,故函数![]() 只有一个零点;
只有一个零点;
② 当![]() 时,
时,![]() ,又
,又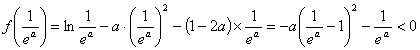 ,
,
![]() ,
,
函数![]() 与
与![]() 轴有两个交点,故函数
轴有两个交点,故函数![]() 有两个零点;
有两个零点;
③ 当![]() 时,
时,![]() ,函数
,函数![]() 与
与![]() 轴没有交点,故函数
轴没有交点,故函数![]() 没有零点.
没有零点.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知函数f(x)=log
[ax2-(a-1)x-2]的值域为R,且f(x)在(2,5)上是减函数,则实数a的取值范围是( )
| 1 |
| 2 |
| A、a>0 | ||
| B、a≥0 | ||
| C、0≤a≤2 | ||
D、-
|
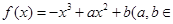 R).
R).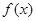 的图象能否总在直线
的图象能否总在直线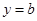 的下方?说明理由;
的下方?说明理由;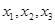 为方程
为方程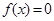 的三个根,且
的三个根,且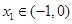 ,
,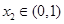 ,
,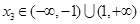 , 求证:
, 求证: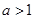 或
或