题目内容
【题目】已知![]() 是一元二次方程
是一元二次方程![]() 的两个实数根.
的两个实数根.
(1)是否存在实数![]() ,使
,使![]() 成立?若存在,求出
成立?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(2)求使![]() 的值为整数的实数
的值为整数的实数![]() 的整数值.
的整数值.
(3)已知对于x的所有实数值,二次函数![]() 的值都是非负的,求关于x的方程
的值都是非负的,求关于x的方程![]() 的根的取值范围
的根的取值范围
【答案】(1)不存在实数![]() (2)
(2)![]() (3)
(3)![]()
【解析】
试题分析:(1)根据已知方程有两个实数根,那么△≥0,可得k的范围,由于方程有两个实数根,那么根据根与系数的关系可得![]() ,然后把
,然后把![]() 代入
代入![]() 中,进而可求k的值;(2)由
中,进而可求k的值;(2)由![]() 是一元二次方程4kx2-4kx+k+2=0的两个实数根,利用根与系数的关系表示出
是一元二次方程4kx2-4kx+k+2=0的两个实数根,利用根与系数的关系表示出![]() ,将
,将![]() 通分并利用同分母分式的加法法则计算,利用完全平方公式变形后,把表示出
通分并利用同分母分式的加法法则计算,利用完全平方公式变形后,把表示出![]() 代入,整理后根据此式子的值为整数,即可求出实数k的整数值;(3)先根据
代入,整理后根据此式子的值为整数,即可求出实数k的整数值;(3)先根据![]() 的值都是非负的,判别式小于等于0求得a的范围,进而根据a的范围确定函数x的解析式,根据函数的单调性求得函数的值域
的值都是非负的,判别式小于等于0求得a的范围,进而根据a的范围确定函数x的解析式,根据函数的单调性求得函数的值域
试题解析:(1)假设存在实数![]() ,使
,使![]() 成立.
成立.
∵ 一元二次方程![]() 的两个实数根
的两个实数根
∴  ,
,
又![]() 是一元二次方程
是一元二次方程![]() 的两个实数根
的两个实数根
∴ 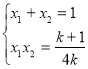
∴![]()
![]() ,但
,但![]() .
.
∴不存在实数![]() ,使
,使![]() 成立.
成立.
(2)∵ ![]()
∴ 要使其值是整数,只需![]() 能被4整除,故
能被4整除,故![]() ,注意到
,注意到![]() ,
,
故要使![]() 的值为整数的实数
的值为整数的实数![]() 的整数值为
的整数值为![]() .
.
(3)![]() 的图像开口向上
的图像开口向上
要![]() 的值都是非负
的值都是非负
即![]()
![]() -
-
①当![]() 时
时
![]()
![]()
![]()
![]()
当![]() 时
时
![]() 的最大值等于
的最大值等于![]()
当![]() 时
时
![]() 的最小值等于
的最小值等于![]()
②当![]() 时
时
![]()
![]()
![]() =
=
当![]() 时
时
![]() 的最小值等于6
的最小值等于6
当![]() 时
时
![]() 的最大值等于12
的最大值等于12
综上所述,![]() 的取值范围是
的取值范围是![]() 。
。

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目