题目内容
(本题满分12分)在数列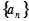 中,已知
中,已知 ,
, (
(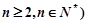 .
.
(1)求证: 是等差数列;
是等差数列;
(2)求数列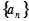 的通项公式
的通项公式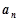 及它的前
及它的前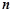 项和
项和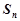 .
.
【答案】
(1)根据已知条件可以得出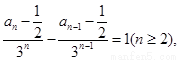
 ,从而可证(2)
,从而可证(2)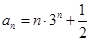 ,
,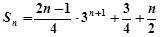
【解析】
试题分析:(1)
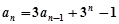 ,
,
即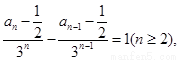 又
又 ,
,
所以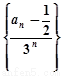 是以1为首项,以1为公差的等差数列.
……5分
是以1为首项,以1为公差的等差数列.
……5分
(2)由(1)知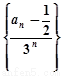 是以1为首项,以1为公差的等差数列,
是以1为首项,以1为公差的等差数列,
∴ 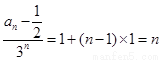 ,∴
,∴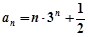 ,
……8分
,
……8分
∴ 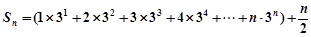 ,
,
令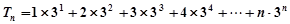 ,
……①
,
……①
则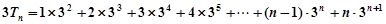 ,
……②
,
……②
两式相减得: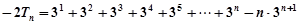

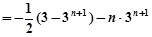 ,
,
所以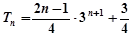 ,所以
,所以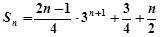 .
……12分
.
……12分
考点:本小题主要考查用定义证明等差数列、等差数列的通项公式、分组法和错位相减法的应用,考查学生的转化能力和运算求解能力.
点评:证明等差数列或者等比数列,尽量要交代首项和公差或首项和公比;错位相减是求数列前n项和的常用方法,要仔细运算.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
 中
中 分别为A,B,C所对的边,
分别为A,B,C所对的边, 且
且

 ,求
,求 的取值范围
的取值范围 中,数列的前n项和
中,数列的前n项和 满足
满足
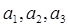 ;(2) 由(1)猜想数列
;(2) 由(1)猜想数列 中,E是BC的中点,F是
中,E是BC的中点,F是 的中点
的中点
 的平面角的余弦值。
的平面角的余弦值。