题目内容
(本题满分12分)在 中
中 分别为A,B,C所对的边,
分别为A,B,C所对的边, 且
且
(1)判断 的形状;
的形状;
(2)若
 ,求
,求 的取值范围
的取值范围
【答案】
(1) 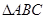 为等腰三角形。
为等腰三角形。
(2) 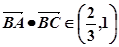
【解析】
试题分析:解:(1)由题意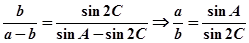
由正弦定理知,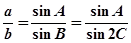 在
在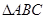 中,
中,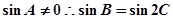
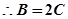 或
或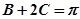
当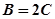 时,
时,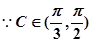
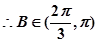 则
则 舍
舍
当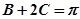 时,
时,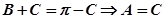 即
即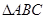 为等腰三角形。
为等腰三角形。
(2)在等腰三角形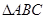 ,
,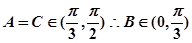
取AC中点D,由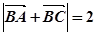 ,得
,得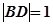
又由,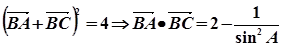
所以,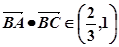
考点:向量的数量积,解三角形综合
点评:解决该试题的关键是对于已知中角的关系式的化简和求解,同时能结合向量的知识来得到其取值范围,属于基础题。

练习册系列答案
相关题目
 中,数列的前n项和
中,数列的前n项和 满足
满足
 ;(2) 由(1)猜想数列
;(2) 由(1)猜想数列 中,E是BC的中点,F是
中,E是BC的中点,F是 的中点
的中点
 的平面角的余弦值。
的平面角的余弦值。