题目内容
已知a∈[-2,2],b∈[0,4],(1)若a∈z,b∈z,求事件A:2a+b≥4的概率;
(2)求P(a,b)满足条件:
|
分析:(1)本小问是关于古典概型的题目,只要利用列举法就可以得出满足条件的概率;
(2)这一问考查几何概型,需要利用坐标系画出不等式组表示的区域,转化为面积之比进行解决.
(2)这一问考查几何概型,需要利用坐标系画出不等式组表示的区域,转化为面积之比进行解决.
解答:解:(1)以(a,b)表a,b的取值个数,则由列举法知:满足a∈[-2,2],b∈[0,4且a∈Z,b∈的所有不同个数共有:5×5=25种;…(2分)
其中事件A:2a+b≥4包含其中的(0,4),(1,2),(1,3),(1,4)(2,0),(2,1),(2,2),(2,3),(2,4)共9种;…(4分)
则P(A)=
.…(5分)
(2)根据题设条件,可Ω={(a,b)|a∈[-2,2],b∈[0,4]},则μ(Ω)=4×4=16;…(6分)
设事B={(a,b)|
a∈[-2,2],b∈[0,4]},则B表示的区域为图中阴影部分;
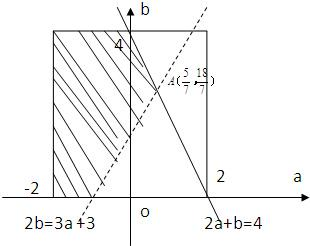 …(8分)
…(8分)
由
得
,即交点坐标(
,
);…(9分)
2b=3a+3;令a=0得b =
;令b=0得a=-1;
μ(B)=
×
×(4-
) +(4×2-
×1×
) =
;…(11分)
P(B)=
=
.…(12分).
其中事件A:2a+b≥4包含其中的(0,4),(1,2),(1,3),(1,4)(2,0),(2,1),(2,2),(2,3),(2,4)共9种;…(4分)
则P(A)=
| 9 |
| 25 |
(2)根据题设条件,可Ω={(a,b)|a∈[-2,2],b∈[0,4]},则μ(Ω)=4×4=16;…(6分)
设事B={(a,b)|
|
 …(8分)
…(8分)由
|
|
| 5 |
| 7 |
| 18 |
| 7 |
2b=3a+3;令a=0得b =
| 3 |
| 2 |
μ(B)=
| 1 |
| 2 |
| 5 |
| 7 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 57 |
| 7 |
P(B)=
| μ(B) |
| μ(Ω) |
| 57 |
| 112 |
点评:本题是考查古典概型和几何概型的题目,古典概型要求所有结果出现的可能性都相等,强调所有结果中每一结果出现的概率都相同.几何概型,一般要通过把试验发生包含的事件同集合结合起来,根据集合对应的图形做出面积,用面积的比值得到结果.

练习册系列答案
相关题目